题目内容
(06年山东卷文)(12分)
已知椭圆的中心在坐标原点O,焦点在x轴上,椭圆的短轴端点和焦点所组成的四边形为正方形,两准线间的距离为l.
(Ⅰ)求椭圆的方程;
(Ⅱ)直线![]() 过点P(0,2)且与椭圆相交于A、B两点,当ΔAOB面积取得最大值时,求直线l的方程.
过点P(0,2)且与椭圆相交于A、B两点,当ΔAOB面积取得最大值时,求直线l的方程.
解析:设椭圆方程为![]()
(Ⅰ)由已知得

∴所求椭圆方程为 ![]() .
.
(Ⅱ)解法一:由题意知直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]()
由 ,消去y得关于x的方程:
,消去y得关于x的方程:![]()
由直线![]() 与椭圆相交于A、B两点,
与椭圆相交于A、B两点,![]()
解得![]() ,又由韦达定理得
,又由韦达定理得
![]()
![]()
原点![]() 到直线
到直线![]() 的距离
的距离![]()
![]() .
.
解法1:对![]() 两边平方整理得:
两边平方整理得:
![]() (*)
(*)
∵![]() ,
, ,整理得:
,整理得:![]()
、又![]() ,
, ![]() ,从而
,从而![]() 的最大值为
的最大值为![]() ,
,
此时代入方程(*)得 ![]()
![]()
所以,所求直线方程为:![]() .
.
解法2:令![]() ,则
,则![]()
 ,当且仅当
,当且仅当![]() 即
即![]() 时,
时,
![]() ,此时
,此时![]() .
.
所以,所求直线方程为![]()
解法二:由题意知直线l的斜率存在且不为零.
设直线l的方程为![]() ,
,
则直线l与x轴的交点![]() ,
,
由解法一知![]() 且
且 ,
,
解法1:![]() =
=![]()
![]()
![]()
![]() .
.
下同解法一.
解法2:![]()
![]()
![]()
![]()
下同解法一.

练习册系列答案
相关题目
 则z=2x+3y的最小值是( )
则z=2x+3y的最小值是( )
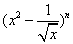 的展开式中第三项与第五项的系数之比为
的展开式中第三项与第五项的系数之比为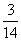 ,则展开式中常数项是( )
,则展开式中常数项是( )