题目内容
已知常数a>0,函数f(x)=
(1)求f(x)的单调递增区间;
(2)若0<a≤2,求f(x)在区间[1,2]上的最小值g(a);
(3)是否存在常数t,使对于任意x∈(
,2t-
)(t>
)时,f(x)f(2t-x)+f2(t)≥[f(x)+f(2t-x)]f(t)恒成立,若存在,求出t的值;若不存在,说明理由.
|
(1)求f(x)的单调递增区间;
(2)若0<a≤2,求f(x)在区间[1,2]上的最小值g(a);
(3)是否存在常数t,使对于任意x∈(
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
(1)当|x|<
时,f(x)=
a2x为增函数. …(1分)
当|x|≥
时,f'(x)=3x2-
.
令f'(x)>0,得x>a或x<-a.…(3分)
∴f(x)的增区间为(-∞,-a),(-
,
)和(a,+∞).…(4分)
(2)函数的图象如图,由图可知,

①当1<a<2时,
<1<a,f(x)在区间[1,a]上递减,在[a,2]上递增,最小值为f(a)=4a3;…(6分)
②当0<a≤1时,f(x)在区间[1,2]为增函数,最小值为f(1)=1+3a4;…(8分)
③当a=2时,f(x)在区间[1,2]为减函数,最小值为f(a)=4a3; …(9分)
综上,f(x)最小值g(a)=
. …(10分)
(3)由f(x)f(2t-x)+f2(t)≥[f(x)+f(2t-x)]f(t),
可得[f(t)-f(x)][f(t)-f(2t-x)]≥0,…(12分)
即
或
成立,所以t为极小值点,或t为极大值点.
又x∈(
,2t-
)时,f(x)没有极大值,所以t为极小值点,即t=a…(16分)
(若只给出t=a,不说明理由,得1分)
| a |
| 2 |
| 49 |
| 4 |
当|x|≥
| a |
| 2 |
| 3a4 |
| x2 |
令f'(x)>0,得x>a或x<-a.…(3分)
∴f(x)的增区间为(-∞,-a),(-
| a |
| 2 |
| a |
| 2 |
(2)函数的图象如图,由图可知,

①当1<a<2时,
| a |
| 2 |
②当0<a≤1时,f(x)在区间[1,2]为增函数,最小值为f(1)=1+3a4;…(8分)
③当a=2时,f(x)在区间[1,2]为减函数,最小值为f(a)=4a3; …(9分)
综上,f(x)最小值g(a)=
|
(3)由f(x)f(2t-x)+f2(t)≥[f(x)+f(2t-x)]f(t),
可得[f(t)-f(x)][f(t)-f(2t-x)]≥0,…(12分)
即
|
|
又x∈(
| a |
| 2 |
| a |
| 2 |
(若只给出t=a,不说明理由,得1分)

练习册系列答案
相关题目

 时,f(x)f(2t-x)+f2(t)≥[f(x)+f(2t-x)]f(t)恒成立,若存在,求出t的值;若不存在,说明理由.
时,f(x)f(2t-x)+f2(t)≥[f(x)+f(2t-x)]f(t)恒成立,若存在,求出t的值;若不存在,说明理由.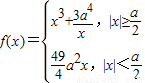
 时,f(x)f(2t-x)+f2(t)≥[f(x)+f(2t-x)]f(t)恒成立,若存在,求出t的值;若不存在,说明理由.
时,f(x)f(2t-x)+f2(t)≥[f(x)+f(2t-x)]f(t)恒成立,若存在,求出t的值;若不存在,说明理由.
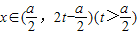 时,f(x)f(2t-x)+f2(t)≥[f(x)+f(2t-x)]f(t)恒成立,若存在,求出t的值;若不存在,说明理由.
时,f(x)f(2t-x)+f2(t)≥[f(x)+f(2t-x)]f(t)恒成立,若存在,求出t的值;若不存在,说明理由.