题目内容
12．函数f（x）=$\frac{\sqrt{x}}{x-1}$的定义域是（ ）| A． | [0，+∞） | B． | [0，1）∪（1，+∞） | C． | （0，1） | D． | （0，1）∪（1，+∞） |
分析 根据函数成立的条件进行求解即可．
解答 解：要使函数有意义，则$\left\{\begin{array}{l}{x≥0}\\{x-1≠0}\end{array}\right.$，即$\left\{\begin{array}{l}{x≥0}\\{x≠1}\end{array}\right.$，
即函数的定义域为[0，1）∪（1，+∞），
故选：B．
点评 本题主要考查函数的定义域的求解，要求熟练掌握常见函数成立的条件．
练习册系列答案
相关题目
20．为了得到函数y=sin（2x-$\frac{π}{4}$）的图象，只要将函数y=sin（x-$\frac{π}{4}$）上所有的点（ ）
| A． | 横坐标伸长到原来的2倍，纵坐标不变 | |
| B． | 横坐标缩短到原来的$\frac{1}{2}$倍，纵坐标不变 | |
| C． | 纵坐标伸长到原来的2倍，横坐标不变 | |
| D． | 纵坐标缩短到原来的$\frac{1}{2}$倍，横坐标不变 |
17．设点F为双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点，直线l过原点且与双曲线C相交于A，B两点，若双曲线C的右顶点M恰为△ABF的重心，则双曲线C的离心率为（ ）
| A． | $\frac{4}{3}$ | B． | $\frac{3}{2}$ | C． | 2 | D． | 3 |
4．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{4}=1（{a＞0}）$与双曲线$\frac{x^2}{9}-\frac{y^2}{3}$=1有相同的焦点，则a的值为（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{10}$ | C． | 4 | D． | 10 |
1．函数f（x）的图象如图所示，下列选项中正确的是（ ）
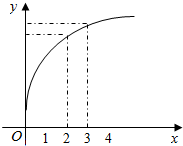
| A． | 0＜f′（2）＜f′（3）＜f（3）-f（2） | B． | 0＜f′（3）＜f′（2）＜f（3）-f（2） | C． | 0＜f′（3）＜f（3）-f（2）＜f′（2） | D． | 0＜f（3）-f（2）＜f′（2）＜f′（3） |