题目内容
(1)设△ABC的顶点A、B在平面α外,顶点C在平面α内,AB在平面α上的射影分别为A1、B1,AA1＜BB1,△ABC的边BC上的高为AD,AD∥平面α,BC与α所成角为θ,求平面ABC与平面α所成角的大小;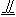
(2)正方体ABCD—A1B1C1D1中,E是BC的中点,求平面B1D1E和平面ABCD所成的二面角的正弦值.
(1)解析：过D作DE⊥B1C于E,?
∵BB1⊥面α,?∴面CBB1⊥面α.?
∴DE⊥面α.∵AA1⊥面α,?
∴AA1∥DE.∴A、A1、E、D四点共面.?
∴A1E AD.∴A1E⊥BC.?
∴A1E⊥B1C.?
∴S△A1CB1=
A1E×B1C?
=
AD×BCcosθ.?
∵AA1、BB1均垂直面α,∴△A1CB1为△ABC在面α上的射影.?
∴设该二面角大小为β.?
∴cosβ=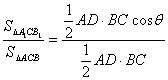
=cosθ.∴α=θ.?
(2)解析：取B1C1中点E1,连结EE1,过E1作E1F⊥B1D1于F,连结EF.?
∵E为BC中点,E1为B1C1中点,?
∴EE1⊥面A1B1C1D1.?
∵面ABCD∥面A1B1C1D1,∴面B1D1E和面ABCD所成角等于面B1D1E与面A1B1C1D1所成角，设为α,并设该立方体边长为a.?
∵△B1E1D1为△B1ED1在面A1B1C1D1内的射影,∴|cosα|=
.∴sinα=
.
练习册系列答案
相关题目
如图，GH是东西方向的公路北侧的边缘线，某公司准备在GH上的一点B的正北方向的A处建一仓库，设AB=y km，并在公路同侧建造边长为x km的正方形无顶中转站CDEF（其中边EF在GH上），现从仓库A向GH和中转站分别修两条道路AB，AC，已知AB=AC+1，且∠ABC=60°．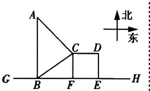
如图所示，GH是一条东西方向的公路，现准备在点B的正北方向的点A处建一仓库，设AB=y千米，并在公路旁边建造边长为x千米的正方形无顶中转站CDEF（其中边EF在公路GH上），现向公路和中转站分别修两条简易公路AB，AC，已知AB=AC+1，且∠ABC=60°．