题目内容
已知二次函数f(x)=ax2+bx+c(a,b,c均为实数),满足a-b+c=0,对于任意实数x 都有f (x)-x≥0,并且当x∈(0,2)时,有f (x)≤![]() .
.
(1)求f (1)的值;
(2)证明:ac≥![]() ;
;
(3)当x∈[-2,2]且a+c取得最小值时,函数F(x)=f (x)-mx (m为实数)是单调的,求证:m≤![]() 或m≥
或m≥![]() .
.
(1)f (1)=1.
(2)见解析
(3)见解析
解析:
(1)∵对于任意x∈R,都有f (x)-x≥0,且当x∈(0,2)时,
有f (x) ≤![]() .令x=1
.令x=1
∴1≤f (1) ≤![]() .
.
即f (1)=1. 5分
(2) 由a-b+c=0及f (1)=1.
有![]() ,可得b=a+c=
,可得b=a+c=![]() . 7分
. 7分
又对任意x,f(x)-x≥0,即ax2-![]() x+c≥0.
x+c≥0.
∴a>0且△≤0.
即![]() -4ac≤0,解得ac≥
-4ac≤0,解得ac≥![]() . 9分
. 9分
(3) 由(2)可知a>0,c>0.
a+c≥2![]() ≥2·
≥2·![]() =
=![]() . 10分
. 10分
当且仅当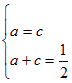 时等号成立.此时
时等号成立.此时
a=c=![]() .
.
∴f (x)= ![]() x2+
x2+![]() x+
x+![]() ,
,
F (x)=f (x)-mx=![]() [x2+(2-4m)x+1]. 12分
[x2+(2-4m)x+1]. 12分
当x∈[-2,2]时,f (x)是单调的,所以F (x)的顶点一定在[-2,2]的外边.
∴![]() ≥2. 13分
≥2. 13分
解得m≤-![]() 或m≥
或m≥![]() . …………………………………………………………..14分
. …………………………………………………………..14分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目