题目内容
(2012•通州区一模)已知函数f(x)=2sinxcosx+2cos2x+1.
(Ⅰ)求f(x)的最小正周期;
(Ⅱ)求f(x)在区间[-
,0]上的最大值和最小值.
(Ⅰ)求f(x)的最小正周期;
(Ⅱ)求f(x)在区间[-
| π | 2 |
分析:(Ⅰ)把函数解析式利用二倍角的正弦、余弦函数公式化简,再利用两角和与差的正弦函数公式积特殊角的三角函数值化为一个角的正弦函数,找出ω的值,代入周期公式,即可求出函数的最小正周期;
(Ⅱ)由x的范围求出这个角的范围,利用正弦函数的图象与性质即可求出f(x)在区间[-
,0]上的最大值与最小值.
(Ⅱ)由x的范围求出这个角的范围,利用正弦函数的图象与性质即可求出f(x)在区间[-
| π |
| 2 |
解答:解:(Ⅰ)f(x)=2sinxcosx+2cos2x+1
=2sinxcosx+2cos2x-1+2=sin2x+cos2x+2=
sin(2x+
)+2,
∵ω=2,∴T=
=π,
则函数f(x)的最小正周期为π;
(Ⅱ)∵x∈[-
,0]时,∴2x+
∈[-
,
],
当2x+
=
,即x=0时,sin(2x+
)=sin
=
,
∴f(x)取得最大值3;
当2x+
=-
,即x=-
时,sin(2x+
)=sin(-
)=-1,
∴f(x)取得最小值2-
.
=2sinxcosx+2cos2x-1+2=sin2x+cos2x+2=
| 2 |
| π |
| 4 |
∵ω=2,∴T=
| 2π |
| 2 |
则函数f(x)的最小正周期为π;
(Ⅱ)∵x∈[-
| π |
| 2 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
当2x+
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
∴f(x)取得最大值3;
当2x+
| π |
| 4 |
| π |
| 2 |
| 3π |
| 8 |
| π |
| 4 |
| π |
| 2 |
∴f(x)取得最小值2-
| 2 |
点评:此题考查了二倍角的正弦、余弦函数公式,两角和与差的正弦函数公式,以及正弦函数的图象与性质,熟练掌握公式是解本题的关键.

练习册系列答案
相关题目
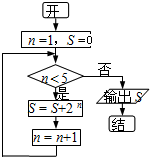 (2012•通州区一模)如图,程序框图所进行的求和运算是( )
(2012•通州区一模)如图,程序框图所进行的求和运算是( )