题目内容
若钝角三角形三内角的度数成等差数列,且最大边长与最小边长的比值为m,则m的范围是________.
m>2
分析:由题意可得B=60°,A+C=120°,由正弦定理结合题意可得 m= =
=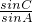 ;由于钝角三角形中,C大于90°
;由于钝角三角形中,C大于90°
可得 0<A<30°,故 0<sinA< ,0<sinC<1,从而得到 m>
,0<sinC<1,从而得到 m> =2.
=2.
解答:设三内角分别为 A,B,C,设C为钝角,则 2B=A+C,∴B=60°,A+C=120°.
由正弦定理可得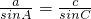 ,
,
根据题意可得 m= =
=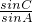 .由于0<sinA<
.由于0<sinA< ,0<sinC<1,∴m>
,0<sinC<1,∴m> =2,
=2,
故答案为m>2.
点评:本题考查正弦定理的应用,大角对大边,正弦函数的值域,判断0<sinA< ,0<sinC<1,是解题的关键.
,0<sinC<1,是解题的关键.
分析:由题意可得B=60°,A+C=120°,由正弦定理结合题意可得 m=
 =
=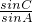 ;由于钝角三角形中,C大于90°
;由于钝角三角形中,C大于90° 可得 0<A<30°,故 0<sinA<
 ,0<sinC<1,从而得到 m>
,0<sinC<1,从而得到 m> =2.
=2.解答:设三内角分别为 A,B,C,设C为钝角,则 2B=A+C,∴B=60°,A+C=120°.
由正弦定理可得
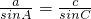 ,
,根据题意可得 m=
 =
=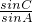 .由于0<sinA<
.由于0<sinA< ,0<sinC<1,∴m>
,0<sinC<1,∴m> =2,
=2,故答案为m>2.
点评:本题考查正弦定理的应用,大角对大边,正弦函数的值域,判断0<sinA<
 ,0<sinC<1,是解题的关键.
,0<sinC<1,是解题的关键. 
练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
若钝角三角形三内角的度数成等差数列,且最大边长与最小边长的比值为m,则m的范围是( )
| A、(1,2) | B、(2,+∞) | C、[3,+∞) | D、(3,+∞) |
若钝角三角形三内角的度数成等差数列,且最大边长与最小边长的比值为m,则m的范围是( )
| A.(1,2) | B.(2,+∞) | C.[3,+∞) | D.(3,+∞) |