Question

P是圆C：x²+y²-2ax+2y+a²=0外的一点，PA、PB为该圆的两条切线，A、B为两切点，那么

PA

•

PB

的最小值为（　　）

• A．-3+2

  2

• B．-3+

  2

• C．-4+2

  2

• D．-4+

  2

Answer 1

分析：由已知中P是圆C：x²+y²-2ax+2y+a²=0外的一点，PA、PB为该圆的两条切线，A、B为两切点，我们设

PC

=X，由切线的性质，易得到

PA

•

PB

的表达式，由基本不等式，即可得到

PA

•

PB

的最小值．

解答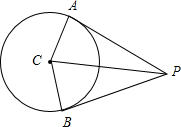：解：∵圆C：x²+y²-2ax+2y+a²=0
可得圆的半径为1，连接CA，CP，CB如下图所示：
设

PC

=X，则|

PA

|=|

PB

|=

X2-1

cos∠APB=cos2∠APC=1-2sin²∠APC=1-

2

X2

∴

PA

•

PB

=（X²-1）•（1-

2

X2

）=-3+（X²+

2

X2

）≥-3+2

2

故

PA

•

PB

的最小值为-3+2

2

故选A

点评：本题考查的知识点是向量在几何中的应用，其中根据已知条件，得到

PA

•

PB

的表达式，将问题转化为一个利用基本不等式求最值的问题，是解答本题的关键．