题目内容
已知定点A(3,4),点P为抛物线y2=4x上一动点,点P到直线x=-1的距离为d,则|PA|+d的最小值为______.
∵抛物线y2=4x的准线方程为x=-1,焦点F坐标(1,0)
因为点A(3,4)在抛物线外,根据抛物线的定义可得
|PA|+d的最小值为|AF|=
=2
故答案为:2
因为点A(3,4)在抛物线外,根据抛物线的定义可得
|PA|+d的最小值为|AF|=
| (3-1)2+(4-0)2 |
| 5 |
故答案为:2
| 5 |

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 上一动点,点P到直线x= -1的距离为d,则
上一动点,点P到直线x= -1的距离为d,则 的最小值是
( )
的最小值是
( )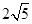 B.2 C.
B.2 C. D.
D.


