题目内容
在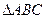 中,
中, 分别为三个内角A、B、C所对的边,设向量
分别为三个内角A、B、C所对的边,设向量
 ,若向量
,若向量 ,则角C的大小为 。
,则角C的大小为 。
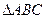 中,
中, 分别为三个内角A、B、C所对的边,设向量
分别为三个内角A、B、C所对的边,设向量
 ,若向量
,若向量 ,则角C的大小为 。
,则角C的大小为 。
本题是向量与解三角形的综合问题,解决的关键是联想余弦定理求解。由 得(a+c)(c-a)=b(b-a),即a2+b2-c2=ab.由余弦定理得
得(a+c)(c-a)=b(b-a),即a2+b2-c2=ab.由余弦定理得 .
.
 得(a+c)(c-a)=b(b-a),即a2+b2-c2=ab.由余弦定理得
得(a+c)(c-a)=b(b-a),即a2+b2-c2=ab.由余弦定理得 .
.
练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
 。
。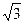 sin
sin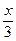 cos
cos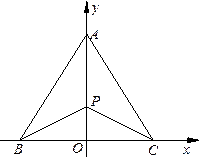 有三个生活小区,分别位于
有三个生活小区,分别位于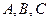 三点处,且
三点处,且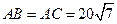 ,
,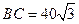 . 今计划合建一个变电站,为同时方便三个小区,准备建在
. 今计划合建一个变电站,为同时方便三个小区,准备建在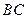 的垂直平分线
的垂直平分线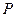 点处,建立坐标系如图,且
点处,建立坐标系如图,且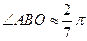 .
.
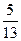 ,求这个三角形的顶角的正弦、余弦及正切值.
,求这个三角形的顶角的正弦、余弦及正切值.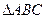 中,若
中,若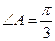 ,AC=2,
,AC=2,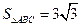 ,则
,则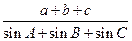 的值为( ).
的值为( ).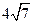
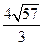
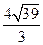

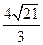
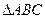 中,角
中,角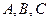 对应的边分别为
对应的边分别为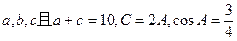
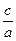 的值 (2)求b的值
的值 (2)求b的值