Question

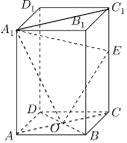
【题目】如图，正四棱柱ABCD﹣A1B1C1D1中，O是BD的中点，E是棱CC1上任意一点．

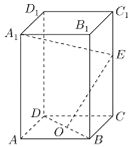
（1）证明：BD⊥A1E；

（2）如果AB=2，，OE⊥A1E，求AA1的长．

Answer 1

【答案】（1）证明见解析（2）

【解析】

（1）根据正四棱柱性质得AA1⊥平面ABCD，即得AA1⊥BD，根据正方形性质的AC⊥BD，再根据线面垂直判定定理得BD⊥平面ACC1A1，即可得结论；

（2）根据勾股定理列等量关系，解得结果.

（1）证明：连结AC，A1C1，

∵AA1⊥平面ABCD，BD平面ABCD，

∴AA1⊥BD，

∵四边形ABCD是正方形，∴AC⊥BD，

又AC∩AA1=A，AC平面ACC1A1，AA1平面ACC1A1，

∴BD⊥平面ACC1A1，又A1E平面ACC1A1，

∴BD⊥A1E．

（2）∵AB=2，∴AO=CO=，A1C1=2，

设AA1=a，则C1E=a﹣，

∴OE2=4，A1O2=a2+2，A1E2=（a﹣）2+8=a2﹣2a+10，

∵OE⊥A1E，

∴A1O2=OE2+A1E2，即a2+2=4+a2﹣2a+10，

解得a=．∴AA1=．