题目内容
（本小题满分10分）
已知数列{
}有以下的特征：
， 
…
是公差为1的等差数列；
…
是公差为
的等差数列；
…
是公差为
的等差数列；……；
…
是公差为
的等差数列（
），其中
．设数列
满足
，
．
(Ⅰ) 求证数列{
}为等比数列；
(Ⅱ) 求数列{}的前
项和
；
(Ⅲ) 当
时，证明对所有正奇数，总有
．
（本小题满分10分）
解：（Ⅰ）证明：当
时，
，
∴ 
． …………………………………… 2分
又
， ∴ 
，……………… 3分
∴ 当
都成立，
故数列{
是以
为首项，
为公比的等比数列． ……………………………4分
（Ⅱ）∵ 
| |
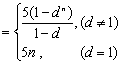…………………………７分 （Ⅲ） 当
时，
显然成立 …………8分
当
， 
，又 
为正奇数 ，∴
故 
，∴ 
． ……………………………………… 10分
或当，又 为正奇数，则
，所以
．
因此，∴ ． ……………………………………… 10分
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
（选做题）本题包括A、B、C、D四小题，请选定其中两题，并在答题卡指定区域内作答，若多做，则按作答的前两题评分，解答时应写出文字说明、证明过程或演算步骤．
本题包括（1）、（2）、（3）、（4）四小题，请选定其中两题，并在答题卡指定区域内答，