题目内容
4.已知:P是直线l:3x+4y+13=0的动点,PA是圆C:x2+y2-2x-2y-2=0的一条切线,A是切点,那么△PAC的面积的最小值是2$\sqrt{3}$.分析 求出圆的标准方程,以及三角形的面积,将面积的最值问题转化为点到直线的距离问题是解决本题的关键.
解答 解:圆的标准方程为(x-1)2+(y-1)2=4,
则圆心坐标为C(1,1),半径R=2,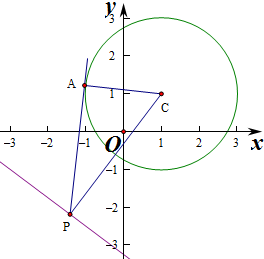
则△PAC的面积S=$\frac{1}{2}PA•AC=\frac{1}{2}×2PA=PA$,
∴要使△PAC的面积的最小,则PA最小,
即PC最小即可,此时最小值为圆心C到直线的距离d=$\frac{|3+4+13|}{\sqrt{{3}^{2}+{4}^{2}}}=\frac{20}{5}=4$,
即PC=d=4,
此时PA=$\sqrt{P{C}^{2}-A{C}^{2}}=\sqrt{16-4}=\sqrt{12}$=2$\sqrt{3}$,
即△PAC的面积的最小值为S=2$\sqrt{3}$,
故答案为:2$\sqrt{3}$
点评 本题主要考查直线和圆的位置关系的应用,将三角形的面积进行转化,以及利用数形结合是解决本题的关键.

练习册系列答案
相关题目
14.设a=log53,b=log73,c=log35,则a,b,c的大小关系是( )
| A. | a>b>c | B. | c>b>a | C. | c>a>b | D. | a>c>b |
15.已知命题p:?x∈R,2x>x2;命题q:?x(-2,+∞),使得(x+1)•ex≤1,则下列命题中为真命题的是( )
| A. | p∧q | B. | p∨(¬q) | C. | (¬p)∧q | D. | (¬p)∧(¬q) |
12.如图,网格上的小正方形的边长为1,粗实线画出的是某几何体的三视图,则该组合体的体积为( )

| A. | 12π+4+4$\sqrt{3}$ | B. | 12π+4$\sqrt{3}$ | C. | 4π+8 | D. | 4π+$\frac{8}{3}$ |
9. (x2+$\frac{a}{2x}$)6展开式的常数项是15,如图阴影部分是由曲线y=x2和圆x2+y2=a及x轴围成的封闭图形,则封闭图形的面积为( )
(x2+$\frac{a}{2x}$)6展开式的常数项是15,如图阴影部分是由曲线y=x2和圆x2+y2=a及x轴围成的封闭图形,则封闭图形的面积为( )
 (x2+$\frac{a}{2x}$)6展开式的常数项是15,如图阴影部分是由曲线y=x2和圆x2+y2=a及x轴围成的封闭图形,则封闭图形的面积为( )
(x2+$\frac{a}{2x}$)6展开式的常数项是15,如图阴影部分是由曲线y=x2和圆x2+y2=a及x轴围成的封闭图形,则封闭图形的面积为( )| A. | $\frac{π}{4}$-$\frac{1}{6}$ | B. | $\frac{π}{4}$+$\frac{1}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{1}{6}$ |
