题目内容
已知三角形PAD所在平面与矩形ABCD所在平面互相垂直，PA=PD=AB=2，∠APD=120°，若点P、A、B、C、D都在同一球面上，则此球的表面积等于分析：设球心为O，如图．由于点P、A、B、C、D都在同一球面上，∴OP=OB=R，设OE=x，分别在直角三角形BOE中，和在直角三角形POH中，列出球的半径的式子，通过解方程求得此球的半径，从而得出表面积．
解答：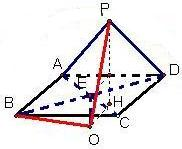
解：设球心为O，如图．
由PA=PD=AB=2，∠APD=120°，可求得AD=2
在矩形ABCD中，可求得对角线BD=4，故BE=2
由于点P、A、B、C、D都在同一球面上，
∴OP=OB=R
设OE=x，在直角三角形BOE中，
OB2=BE2+OE2=4+x2
过O作线段OH垂直平面PAD于H点，H是垂足，由于O点到面PAD的距离与点E到平面PAD的距离相等，故OH=1
∴在直角三角形POH中，PO2=OH2+PH2=1+（1+x）2
∴4+x2=1+（1+x）2，解得x=1，
∴球的半径R=OB=
则此球的表面积等于=4πR2=20π．
故答案为：20π．
解：设球心为O，如图．由PA=PD=AB=2，∠APD=120°，可求得AD=2
| 3 |
在矩形ABCD中，可求得对角线BD=4，故BE=2
由于点P、A、B、C、D都在同一球面上，
∴OP=OB=R
设OE=x，在直角三角形BOE中，
OB2=BE2+OE2=4+x2
过O作线段OH垂直平面PAD于H点，H是垂足，由于O点到面PAD的距离与点E到平面PAD的距离相等，故OH=1
∴在直角三角形POH中，PO2=OH2+PH2=1+（1+x）2
∴4+x2=1+（1+x）2，解得x=1，
∴球的半径R=OB=
| 5 |
则此球的表面积等于=4πR2=20π．
故答案为：20π．
点评：本题是基础题，考查球的体积和表面积，解题的根据是点P、A、B、C、D都在同一球面上，考查计算能力，空间想象能力．
练习册系列答案
相关题目