题目内容
函数 的单调递减区间是________.
的单调递减区间是________.
(-2,2)
分析:先求出原函数的定义域,然后把原函数分解为两基本函数y=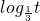 和t=-x2+4x+12,
和t=-x2+4x+12,
由复合函数单调性的判定方法知,要求原函数的减区间只需在定义域内求出t=-x2+4x+12的增区间即可.
解答:由-x2+4x+12>0,解得-2<x<6,即原函数的定义域为(-2,6).
原函数可看作由函数y=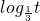 和t=-x2+4x+12复合而成的,
和t=-x2+4x+12复合而成的,
因为函数y=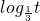 单调递减,所以,要求原函数的减区间只需求出t=-x2+4x+12的增区间,
单调递减,所以,要求原函数的减区间只需求出t=-x2+4x+12的增区间,
而t=-x2+4x+12=-(x-2)2+16的增区间为(-2,2).
所以原函数的单调减区间是(-2,2).
故答案为:(-2,2).
点评:本题考查复合函数单调性的判定及对数函数的单调性,注意复合函数单调性的判定方法:同增异减.
分析:先求出原函数的定义域,然后把原函数分解为两基本函数y=
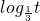 和t=-x2+4x+12,
和t=-x2+4x+12,由复合函数单调性的判定方法知,要求原函数的减区间只需在定义域内求出t=-x2+4x+12的增区间即可.
解答:由-x2+4x+12>0,解得-2<x<6,即原函数的定义域为(-2,6).
原函数可看作由函数y=
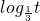 和t=-x2+4x+12复合而成的,
和t=-x2+4x+12复合而成的,因为函数y=
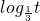 单调递减,所以,要求原函数的减区间只需求出t=-x2+4x+12的增区间,
单调递减,所以,要求原函数的减区间只需求出t=-x2+4x+12的增区间,而t=-x2+4x+12=-(x-2)2+16的增区间为(-2,2).
所以原函数的单调减区间是(-2,2).
故答案为:(-2,2).
点评:本题考查复合函数单调性的判定及对数函数的单调性,注意复合函数单调性的判定方法:同增异减.

练习册系列答案
相关题目

 的单调递减区间是 .
的单调递减区间是 .  的单调递减区间是 . (科网
的单调递减区间是 . (科网