题目内容
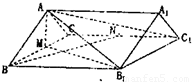
 如图,已知四棱柱ABCD-A1B1C1D1的底面是菱形,侧棱BB1⊥底面ABCD,E是侧棱CC1的中点.
如图,已知四棱柱ABCD-A1B1C1D1的底面是菱形,侧棱BB1⊥底面ABCD,E是侧棱CC1的中点.(Ⅰ)求证:AC⊥平面BDD1B1;
(Ⅱ)求证:AC∥平面B1DE.
分析:(Ⅰ)先证AC⊥BD与BB1⊥AC,再证AC⊥平面BDD1B1
(Ⅱ)设AC,BD交于点O,取B1D的中点F,连接OF,EF,先证OF∥CC1与OF=CC1,再证OC∥EF,再证AC∥平面B1DE.
(Ⅱ)设AC,BD交于点O,取B1D的中点F,连接OF,EF,先证OF∥CC1与OF=CC1,再证OC∥EF,再证AC∥平面B1DE.
解答: 证明:(Ⅰ)因为ABCD是菱形,所以AC⊥BD,
证明:(Ⅰ)因为ABCD是菱形,所以AC⊥BD,
因为BB1⊥底面ABCD,
所以BB1⊥AC,(3分)
所以AC⊥平面BDD1B1.(5分)
(Ⅱ)设AC,BD交于点O,取B1D的中点F,连接OF,EF,
则OF∥BB1,且OF=
BB1,
又E是侧棱CC1的中点,EC=
CC1,BB1∥CC1,BB1=CC1,
所以OF∥CC1,且OF=
CC1,(7分)
所以四边形OCEF为平行四边形,OC∥EF,(9分)
又AC∥平面B1DE,EF∥平面B1DE,(11分)
所以AC∥平面B1DE.(13分)
 证明:(Ⅰ)因为ABCD是菱形,所以AC⊥BD,
证明:(Ⅰ)因为ABCD是菱形,所以AC⊥BD,因为BB1⊥底面ABCD,
所以BB1⊥AC,(3分)
所以AC⊥平面BDD1B1.(5分)
(Ⅱ)设AC,BD交于点O,取B1D的中点F,连接OF,EF,
则OF∥BB1,且OF=
| 1 |
| 2 |
又E是侧棱CC1的中点,EC=
| 1 |
| 2 |
所以OF∥CC1,且OF=
| 1 |
| 2 |
所以四边形OCEF为平行四边形,OC∥EF,(9分)
又AC∥平面B1DE,EF∥平面B1DE,(11分)
所以AC∥平面B1DE.(13分)
点评:证明线面垂直的关键是在平面内找到两条相交直线与已知直线垂直,在证明时要充分利用平面几何的知识,以达到通过平面内的垂直关系证明空间中的垂直关系的目的.

练习册系列答案
相关题目
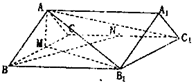 如图,已知直棱柱ABC-A1B1C1中,AB=AC=5,BC=BB1=8,M,N分别为棱BC,CC1的中点.
如图,已知直棱柱ABC-A1B1C1中,AB=AC=5,BC=BB1=8,M,N分别为棱BC,CC1的中点. (2007•无锡二模)如图,已知四棱柱ABCD-A1B1C1D1的底面ABCD为直角梯形,AB∥CD,AB⊥AD,AB=AD=A1B=2CD,侧面A1ADD1为正方形.
(2007•无锡二模)如图,已知四棱柱ABCD-A1B1C1D1的底面ABCD为直角梯形,AB∥CD,AB⊥AD,AB=AD=A1B=2CD,侧面A1ADD1为正方形.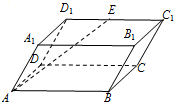 如图,已知四棱柱ABCD-A1B1C1D1的底面ABCD是矩形,AB=4,AA1=3,∠BAA1=60°,E为棱C1D1的中点,则
如图,已知四棱柱ABCD-A1B1C1D1的底面ABCD是矩形,AB=4,AA1=3,∠BAA1=60°,E为棱C1D1的中点,则