题目内容
定义集合P={x|x=3k+1，x∈Z}，Q={x|x=3k-1，x∈Z}，M={x=3k，x∈Z}，若a∈P，b∈Q，c∈N，则a2+b-c∈（ ）
| A、P | B、M | C、Q | D、P∪Q |
考点：元素与集合关系的判断
专题：计算题,集合
分析：集合中元素具有集合中元素的属性设出a、b、c，求出a2+b-c并将其化简，判断即可．
解答：解：∵a∈P，b∈Q，c∈M，
设a=3k1+1，k1∈Z，b=3k2-1，k2∈Z，c=3k3，k3∈Z
∴a2+b-c=（3k1+1）2+3k2-1-3k3=3（3k12+2k1+k2-k3）∈M，
故选：B．
设a=3k1+1，k1∈Z，b=3k2-1，k2∈Z，c=3k3，k3∈Z
∴a2+b-c=（3k1+1）2+3k2-1-3k3=3（3k12+2k1+k2-k3）∈M，
故选：B．
点评：本题考查集合中的元素具有集合的公共属性、元素与集合关系的判断等基础知识，考查化归与转化思想．
练习册系列答案
相关题目
设集合A={1，2，4}，集合B={x|x=a+b，a∈A，b∈A}，则集合B中有（ ）个元素．
| A、4 | B、5 | C、6 | D、7 |
由元素1，2，3组成的集合可记为（ ）
| A、{x=1，2，3} | B、{x=1，x=2，x=3} | C、{x|x∈N+，x＜4} | D、{6的质因数} |
| 256 |
| A、{16} |
| B、{-16，16} |
| C、{4} |
| D、{-4，4} |
已知集合 A={x|x2-2x＜0}，B={1，a}，且A∩B有4个子集，则a的取值范围是（ ）
| A、（0，1） | B、（0，2） | C、（0，1）∪（1，2） | D、（-∞，1）（2，+∞） |
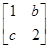有特征值λ1＝4及对应的一个特征向量e1＝
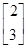.求：
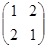的特征值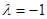
所对应的一个特征向量。
，则
.