题目内容
在正方体ABCD－A1B1C1D1，设M、N、E、F分别是棱A1B1、A1D1、C1D1、B1C1的中点，如图所示．
(1)求证：E、F、B、D四点共面；
(2)求证：平面AMN∥平面EFBD.
(1)分别连结BD、ED、FB，由正方体性质知，B1D1∥BD.
∵E、F分别是C1D1和B1C1的中点，
∴EF綊
B1D1，EF綊BD.
∴E、F、B、D四点共面．
(2)连结A1C1交MN于P点，交EF于点Q，分别连结PA、QO.∵M1N分别为A1B1、A1D1的中点，
∴MN∥EF，EF⊂面EFBD，∴MN∥面EFBD.
∵PQ綊AQ，∴四边形PAOQ为平行四边形，
∴PA∥QO.而QO⊂面EFBD，
∵PA∥面EFBD，且PA∩MN＝P，PA、MN⊂面AMN，
∴平面AMN∥面EFBD.
练习册系列答案
阅读快车系列答案
相关题目
在正方体ABCD-A1B1C1D1中，E是棱A1B1的中点，则A1B与D1E所成角的余弦值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在正方体ABCD-A1B1C1D1中，AB与平面A1BC1所成角的正弦值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
（本小题满分12分）
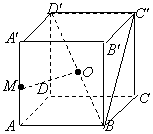
在正方体ABCD－A′B′C′D′中，点M是棱AA′的中点，点O是对角线BD′的中点.
（Ⅰ）求证：OM为异面直线AA′和BD′的公垂线；
（Ⅱ）求二面角M－BC′－B′的大小；
（Ⅰ）求证：OM为异面直线AA′和BD′的公垂线；
（Ⅰ）求证：OM为异面直线AA′和BD′的公垂线；