Question

如图，直线l₁和l₂相交于点M，l₁⊥l₂，点N∈l₁.以A、B为端点的曲线段C上的任一点到l₂的距离与到点N的距离相等.若△AMN为锐角三角形，|AM|=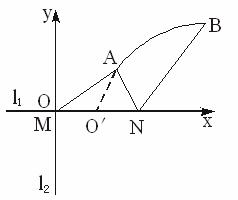，|AN|=3，且|BN|=6.建立适当的坐标系，求曲线段C的方程.

Answer 1

解法一:以l₁为x轴，MN的中点O为原点建立如图的直角坐标系.由题意可知，曲线段C所在的抛物线在直角坐标系中的位置是标准的，并且点N是该抛物线的焦点，l₂是准线.所以可令抛物线的方程为y²=2px(p＞0).过点A作AQ⊥l₂，AE⊥l₁，垂足分别为Q和E，由于△AMN是锐角三角形，则点E必在线段MN上.所以，|AQ|=|AN|=3.

∵|AM|=,

∴|QM|==2,

|AE|=|QM|=2,

|EN|==1.

∴p=|MN|=|ME|+|EN|=|AQ|+|EN|=4.

∴抛物线方程为y²=8x.

由上述可知,|OE|=1，点B到准线l₂的距离为6，则点B的横坐标为4，又曲线段在x轴上方，故曲线段C的方程为

y²=8x(1≤x≤4,y＞0).

解法二:以l₁为x轴，l₂为y轴建立如下图的直角坐标系，其中M点为原点，这时焦点N在x轴上，顶点O′应是线段MN的中点.令曲线段C所在的抛物线方程为.

y²=2p(x－x)(p＞0).

设A(+,y₁),B(+,y₂),则

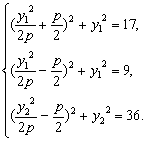
由①－②得y₁²=8,

代入①得(+)²=9.∴8+p²=6p.

∵p＞3,∴p=4.

∵y₁＞0,∴y₁=2.

代入③得y₂=4.

∴曲线段C的方程为y²=8(x－2)(2≤y≤4).

点评:该例题给出的条件比较简明、直接，由抛物线的概念，可知曲线段C是一段抛物线.因此，入手不难,关键的问题是怎样建立适当的坐标系，使得解答过程简单.此例还应注意方程中x或y的取值范围.