题目内容
梯形ABCD的两腰AD和BC的延长线相交于E,若梯形两底的长度分别是12和8,梯形ABCD的面积为90,则△DCE的面积为( )
| A、50 | B、64 | C、72 | D、54 |
分析:如图所示.过点E作EN⊥AB交AB于N点,交CD于点M.利用梯形的面积计算公式可得MN=9.利用AB∥DC,可得
=
,再利用
=(
)2=
=(
)2,即可解得.
| EM |
| EN |
| DC |
| AB |
| S△DCE |
| S△ABE |
| 2 |
| 3 |
| 4 |
| 9 |
| S△DCE |
| S△ABE |
| EM |
| EN |
解答:解:如图所示.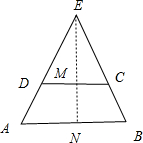
过点E作EN⊥AB交AB于N点,交CD于点M.
∵梯形ABCD的面积为90,∴90=
,解得MN=9.
∵AB∥DC,∴
=
=
=
,
∴
=(
)2=
,∴
=
,
解得S△DCE=72.
故选:C.

过点E作EN⊥AB交AB于N点,交CD于点M.
∵梯形ABCD的面积为90,∴90=
| (8+12)•MN |
| 2 |
∵AB∥DC,∴
| EM |
| EN |
| DC |
| AB |
| 8 |
| 12 |
| 2 |
| 3 |
∴
| S△DCE |
| S△ABE |
| 2 |
| 3 |
| 4 |
| 9 |
| S△DCE |
| S△DCE+90 |
| 4 |
| 9 |
解得S△DCE=72.
故选:C.
点评:本题考查了梯形的面积计算公式、平行线分线段成比例定理、相似三角形的面积比等于相似比的平方等性质,属于基础题.

练习册系列答案
相关题目
