题目内容
若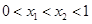 ,则( )
,则( )
A.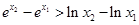 | B.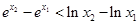 |
C.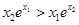 | D.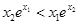 |
C
解析试题分析:(1)欲探究 的大小关系,即探究
的大小关系,即探究 的大小关系,即函数
的大小关系,即函数 的单调性问题。由
的单调性问题。由 可得
可得 .令
.令 则
则 ,当
,当 时,
时, ,且
,且 ,所以
,所以 在
在 有唯一零点
有唯一零点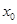 。所以
。所以 在
在 单调递减,
单调递减, 单调递增。故当
单调递增。故当 ,
, ;当
;当 ,
, ;当
;当 ,
, 的关系不确定。综上
的关系不确定。综上 的关系不确定。
的关系不确定。
(2)欲探究 的大小关系,即探究
的大小关系,即探究 的大小关系,有几何关系可看做函数
的大小关系,有几何关系可看做函数 上一点
上一点
 与原点连线的斜率,即
与原点连线的斜率,即 ,因
,因 ,所以
,所以 ,故选C。
,故选C。
考点:(1)利用函数单调性判断大小;(2)化归与转化书序思想;(3)数形结合

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若实数a,b,c,d满足a>b,c>d,则下列不等式成立的是( ).
| A.a﹣c>b﹣d | B.a+c>b+d | C.ac>bd | D. > > |
设 ,
, ,
, ,(e是自然对数的底数),则
,(e是自然对数的底数),则
A. | B. | C. | D. |
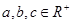 ,设
,设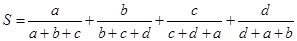 ,则下列判断中正确的是( )
,则下列判断中正确的是( )
A.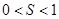 | B.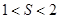 | C.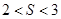 | D. |
已知 且
且 ,则“
,则“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
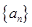 是等差数列,数列
是等差数列,数列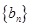 是等比数列,且对任意的
是等比数列,且对任意的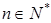 ,都有
,都有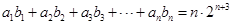 .
.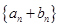 的前
的前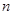 项和
项和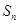 ;
;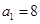 .
.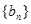 中是否存在某一项,它可以表示为该数列中其它
中是否存在某一项,它可以表示为该数列中其它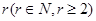 项的和?若存在,请求出该项;若不存在,请说明理由.
项的和?若存在,请求出该项;若不存在,请说明理由.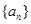 是公比大于1的等比数列,
是公比大于1的等比数列, 为数列
为数列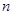 项和。
项和。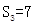 ,且
,且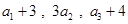 构成等差数列.
构成等差数列.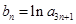 ,求数列
,求数列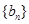 的前
的前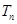 .
.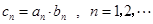 ,求数列
,求数列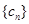 的前
的前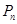 .
.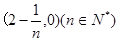 且方向向量为
且方向向量为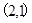 的直线交椭圆
的直线交椭圆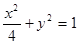 于
于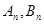 两点,记原点为
两点,记原点为 ,
,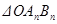 面积为
面积为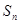 ,则
,则 _______
_______ .
.