Question

实系数方程x²+bx-2c=0有两实根，其中一根x₁∈(-1,0)，另一根x₂∈(0,1)，则的取值范围是(    )

A.（,）                          B.(,)

C.(,1)                               D.(1,+∞)∪(-∞,)

Answer 1

解析：设f(x)=x²+bx-2c.

∵x²+bx-2c=0有两根x₁,x₂,x₁∈(-1,0),x₂∈(0,1)

∴

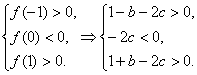
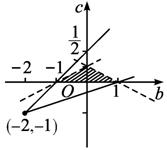
    由点(b,c)满足的平面区域如图所示，∴k=∈(,1).

答案：C