题目内容
椭圆 的离心率为
的离心率为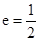 ,右焦点为
,右焦点为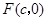 ,方程
,方程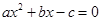 的两个实根分别为
的两个实根分别为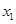 和
和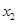 ,则点
,则点 ( )
( )
A.必在圆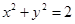 内 内 | B.必在圆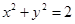 上 上 |
C.必在圆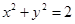 外 外 | D.以上三种情形都有可能 |
A
解析考点:椭圆的简单性质;点与圆的位置关系.
专题:计算题.
分析:由题意可求得c= 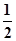 a,b=
a,b= 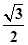 a,从而可求得x1和x2,利用韦达定理可求得x12+x22的值,从而可判断点P与圆x2+y2=2的关系.
a,从而可求得x1和x2,利用韦达定理可求得x12+x22的值,从而可判断点P与圆x2+y2=2的关系.
解答:解:∵椭圆的离心率e=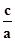 =
=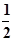 ,
,
∴c=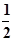 a,b=
a,b=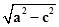 =
=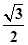 a,
a,
∴ax2+bx-c=ax2+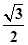 ax-
ax-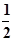 a=0,
a=0,
∵a≠0,
∴x2+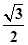 x-
x-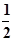 =0,又该方程两个实根分别为x1和x2,
=0,又该方程两个实根分别为x1和x2,
∴x1+x2=-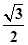 ,x1x2=-
,x1x2=-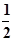 ,
,
∴x12+x22=(x1+x2)2-2x1x2=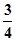 +1<2.
+1<2.
∴点P在圆x2+y2=2的内部.
故选A.
点评:本题考查椭圆的简单性质,考查点与圆的位置关系,求得c,b与a的关系是关键,属于中档题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
抛物线 的焦点坐标是:
的焦点坐标是:
| A.(0,-1) | B.(0,1) | C.(1,0) ( | D.(-1,0) |
双曲线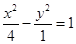 的渐近线方程是
的渐近线方程是
A.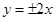 | B.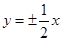 | C.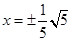 | D.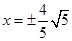 |
抛物线 上的点到直线
上的点到直线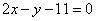 距离的最小值是 ( )
距离的最小值是 ( )
A. | B.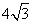 | C.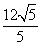 | D.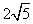 |
已知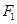 、
、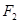 为双曲线C:
为双曲线C: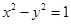 的左、右焦点,点P在C上,∠
的左、右焦点,点P在C上,∠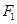
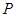
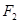 =
=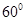 ,则
,则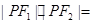 ( *** )
( *** )
| A.2 | B.4 | C.6 | D.8 |
若曲线 与直线
与直线 +3有两个不同的公共点,则实数 k 的取值范围是( )
+3有两个不同的公共点,则实数 k 的取值范围是( )
A.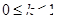 | B.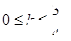 | C.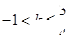 | D.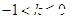 |
设椭圆 ,右焦点F(c,0),方程
,右焦点F(c,0),方程 的两个根分别为x1,x2,则点P(x1,x2)在 ( )
的两个根分别为x1,x2,则点P(x1,x2)在 ( )
A.圆 上 上 | B.圆 内 内 |
C.圆 外 外 | D.以上三种情况都有可能 |
已知椭圆 ,以椭圆的焦点为顶点,顶点为焦点的双曲线方程是
,以椭圆的焦点为顶点,顶点为焦点的双曲线方程是
A. | B. | C.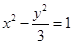 | D. |
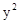 = 2px(p>0)的焦点F作一条直线l交抛物线于A、B两点,以AB为直径的圆和该抛物线的准线l的位置关系是( )
= 2px(p>0)的焦点F作一条直线l交抛物线于A、B两点,以AB为直径的圆和该抛物线的准线l的位置关系是( )