Question

（本小题满分12分）如图，点A，B分别是椭圆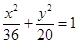的长轴的左右端点，点F为椭圆的右焦点，直线PF的方程为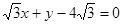：且.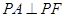

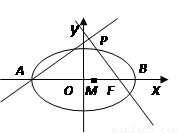
(1)求直线AP的方程；

(2)设点M是椭圆长轴AB上一点，点M到直线AP的距离等于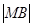，求椭圆上的点到点M的距离d的最小值.

 

Answer 1

【答案】

⑴.⑵当时，，即.

【解析】本题主要考查了直线方程的点斜式在求解直线方程中的应用，结合椭圆的范围求解二次函数的最值，属于知识的简单综合。、

（I）由题设知A（-6，0），直线AP的斜率为 ，从而可得直线AP的方程

（2），则点M到直线AP的距离为，

而，依题意得

得到m的值，然后设椭圆上一点，则，即

得到d²的值。

解： ⑴由题意知，，从而 ，由题意得，，从而，，  ……….…………………………....（2分）

因此，直线AP的方程为：， 即.……….…...（4分）

⑵设，则点M到直线AP的距离为，

而，依题意得

解得或（舍去），故.….………………………..…………....（7分）

设椭圆上一点，则，即

，，……………….…....（10分）

所以当时，，即.-…………………………..………....（12分）