题目内容
如图，三棱锥P-ABC中，AB⊥BC，∠BAC=30°，BC=5，且PA=PB=PC=AC．则点P到平面ABC的距离是________．
5
分析：由题意确定P在底面ABC的射影位置，通过题目数据，求出点P到平面ABC的距离．
解答：
解：因为PA=PB=PC，则它们在平面ABC的射影相等，
P在ABC平面射影应在三角形ABC的外心，
而三角形ABC是直角三角形，
故外心应在斜边的中点D上，
PD⊥底面ABC，∠BAC=30°，AC=2BC=10，BD=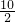
=5，PB=AC=10，
三角形PBD是直角三角形，
根据勾股定理，PD2=PB2-BD2，
PD=5，PD就是P至平面ABC的距离．
故答案为：5．
点评：本题是中档题，考查点到平面的距离的求法，找出点到平面的距离是解题的关键，考查计算能力．
分析：由题意确定P在底面ABC的射影位置，通过题目数据，求出点P到平面ABC的距离．
解答：
解：因为PA=PB=PC，则它们在平面ABC的射影相等，P在ABC平面射影应在三角形ABC的外心，
而三角形ABC是直角三角形，
故外心应在斜边的中点D上，
PD⊥底面ABC，∠BAC=30°，AC=2BC=10，BD=
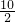=5，PB=AC=10，三角形PBD是直角三角形，
根据勾股定理，PD2=PB2-BD2，
PD=5
，PD就是P至平面ABC的距离．故答案为：5
．点评：本题是中档题，考查点到平面的距离的求法，找出点到平面的距离是解题的关键，考查计算能力．
练习册系列答案
相关题目
如图，三棱锥P-ABC中，PC⊥平面ABC，PC=AC=2，AB=BC，D是PB上一点，且CD⊥平面PAB
（2006•石景山区一模）如图，三棱锥P-ABC中，
（2012•湖南模拟）如图，三棱锥P-ABC中，侧面PAC⊥底面ABC，∠APC=90°，且AB=4，AP=PC=2，BC=2
（2012•德阳二模）如图，三棱锥P-ABC中，PA丄面ABC，∠ABC=90°，PA=AB=1，BC=2，则P-ABC的外接球的表面积为
如图在三棱锥P-ABC中，AB⊥PC，AC=2，BC=4，