题目内容
给出下列命题:
(1)函数f(x)=4sin(2x+ )的图象关于点(-
)的图象关于点(- )对称;
)对称;
(2)函数g(x)=-3sin(2x- )在区间(-
)在区间(- )内是增函数;
)内是增函数;
(3)函数h(x)=sin( x-
x-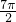 )是偶函数;
)是偶函数;
(4)存在实数x,使sinx+cosx= .
.
其中正确的命题的序号是________.
解:当x=- 时,函数f(x)=4sin(2x+
时,函数f(x)=4sin(2x+ )=0,故点(-
)=0,故点(- )是函数图象与x轴的交点,故函数图象关于点(-
)是函数图象与x轴的交点,故函数图象关于点(- )对称,故(1)正确.
)对称,故(1)正确.
(2)由于函数g(x)=-3sin(2x- ),由 2kπ+
),由 2kπ+ ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈z,
,k∈z,
可得kπ+ ≤x≤kπ+
≤x≤kπ+ ,k∈z,取k=-1,得
,k∈z,取k=-1,得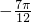 ≤x≤-
≤x≤- ,
,
故函数的增区间为[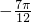 ,-
,- ],故(2)不正确.
],故(2)不正确.
(3)由于h(x)=sin( -
-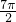 )=cos
)=cos ,从而h(-x)=h(x),得h(x)是偶函数,∴命题(3)正确;
,从而h(-x)=h(x),得h(x)是偶函数,∴命题(3)正确;
(4)中令y=sinx+cosx= sin(x+
sin(x+ )则-
)则- ≤y≤
≤y≤ ,
,
∵- ≤
≤ ≤
≤ ,∴存在实数x,使得sinx+cosx=
,∴存在实数x,使得sinx+cosx= ;即(4)正确.
;即(4)正确.
其中正确的命题的序号是 (1)(3)(4).
故答案为:(1)(3)(4).
分析:根据点(- )是函数图象与x轴的交点,故函数图象关于点(-
)是函数图象与x轴的交点,故函数图象关于点(- )对称,故(1)正确;
)对称,故(1)正确;
由 2kπ+ ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈z,可得y=sin(2x-
,k∈z,可得y=sin(2x- ) 的增区间,可得(2)不正确;
) 的增区间,可得(2)不正确;
对于(3),利用诱导公式化简为y=-cosx,该函数是偶函数;(3)正确;
(4)根据辅助角公式,我们可将sinx+cosx化为 sin(x+
sin(x+ ),再由正弦型函数的值域,可以判断(4)的真假.
),再由正弦型函数的值域,可以判断(4)的真假.
点评:本题主要考查正弦函数的奇偶性、对称性、单调性,判断命题的真假,以及y=Asin(ωx+∅)图象与性质,掌握y=Asin(ωx+∅)图象和性质是解题的关键.属于中档题.
 时,函数f(x)=4sin(2x+
时,函数f(x)=4sin(2x+ )=0,故点(-
)=0,故点(- )是函数图象与x轴的交点,故函数图象关于点(-
)是函数图象与x轴的交点,故函数图象关于点(- )对称,故(1)正确.
)对称,故(1)正确.(2)由于函数g(x)=-3sin(2x-
 ),由 2kπ+
),由 2kπ+ ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈z,
,k∈z,可得kπ+
 ≤x≤kπ+
≤x≤kπ+ ,k∈z,取k=-1,得
,k∈z,取k=-1,得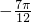 ≤x≤-
≤x≤- ,
,故函数的增区间为[
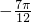 ,-
,- ],故(2)不正确.
],故(2)不正确.(3)由于h(x)=sin(
 -
-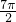 )=cos
)=cos ,从而h(-x)=h(x),得h(x)是偶函数,∴命题(3)正确;
,从而h(-x)=h(x),得h(x)是偶函数,∴命题(3)正确;(4)中令y=sinx+cosx=
 sin(x+
sin(x+ )则-
)则- ≤y≤
≤y≤ ,
,∵-
 ≤
≤ ≤
≤ ,∴存在实数x,使得sinx+cosx=
,∴存在实数x,使得sinx+cosx= ;即(4)正确.
;即(4)正确.其中正确的命题的序号是 (1)(3)(4).
故答案为:(1)(3)(4).
分析:根据点(-
 )是函数图象与x轴的交点,故函数图象关于点(-
)是函数图象与x轴的交点,故函数图象关于点(- )对称,故(1)正确;
)对称,故(1)正确;由 2kπ+
 ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈z,可得y=sin(2x-
,k∈z,可得y=sin(2x- ) 的增区间,可得(2)不正确;
) 的增区间,可得(2)不正确;对于(3),利用诱导公式化简为y=-cosx,该函数是偶函数;(3)正确;
(4)根据辅助角公式,我们可将sinx+cosx化为
 sin(x+
sin(x+ ),再由正弦型函数的值域,可以判断(4)的真假.
),再由正弦型函数的值域,可以判断(4)的真假.点评:本题主要考查正弦函数的奇偶性、对称性、单调性,判断命题的真假,以及y=Asin(ωx+∅)图象与性质,掌握y=Asin(ωx+∅)图象和性质是解题的关键.属于中档题.

练习册系列答案
相关题目