Question

如图7,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2a,AB=a,F为CE的中点.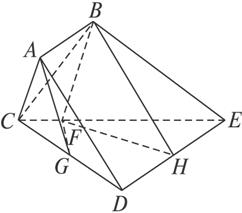

                        图7

(1)求证:BF⊥面CDE.

(2)求多面体ABCDE的体积.

(3)求平面BCE和平面ACD所成的锐二面角的大小.

Answer 1

思路分析:(1)如图7,取CD的中点G,DE的中点H,连接FG,FH,容易证明它们也是相应边的垂线.再连接BH.欲证线面垂直,先证线线垂直.如果BF⊥面CDE证明成立的话,则必然有BF⊥CE,考虑到F为CE的中点,我们的目标就是要证明△BCE是等腰三角形.另外由于BF在平面ACD上的射影AG是△ADC的边CD上的高,所以BF⊥CD.这样BF就垂直于平面ACD上的两条相交直线,从而BF⊥面CDE.(2)求多面体的体积可以采取将图形通过切割转化为几个简单的几何体分别求体积后求和的方法.(3)注意到△BCE在平面ACD上的射影就是△ADC,有结论:两者的面积之比就是所成二面角的余弦值,利用这个结论列式求解.

解:(1)证明:∵AB⊥平面ACD,∴AB⊥AC,

由AB=a,AC=2a,得BC=a.

同理,在直角梯形ABDE中,AB⊥AD,DE⊥AD,且AB=a,AD=DE=2a,所以BE=a.

又F是CE的中点,∴BF⊥CE.

∵BF在面ACD上的射影是等边△ADC的边CD上的高,

∴BF⊥CD.

∴BF⊥平面CDE.

(2)解:连结BD,把原几何体分成三棱锥B—ACD与三棱锥B—CDE.

V_B—ACD=AB·S_ACD=·a·(2a)²=a³.

∵CE=a,CF=a,

而BC=a,∴BF=a,

∴V_B—CDE=BF·S_CDE=·a··(2a)²=.

故所求多面体ABCDE的体积为a³.

(3)解:设面BCE与面ACD所成的角为θ.

∵△BCE在面ACD上的射影为△ACD,

∴cosθ=,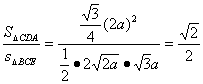

∴θ=