题目内容
10、如图，AB是圆O的直径，D为圆O上一点，过D作圆O的切线交AB延长线于点C，若DA=DC，则∠DAC=
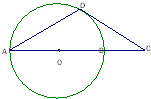
30°
分析：连接BD，由已知中AB是圆O的直径，D为圆O上一点，过D作圆O的切线交AB延长线于点C，若DA=DC，结合圆周角定理的推论，及弦切角定理，及等腰三角形的性质，我们易求出∠DAC的大小．
解答：解：连接BD，如下图所示：
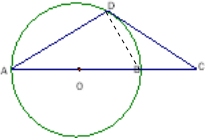
由已知中AB为圆O的直径，则∠ADB=90°
∠A+∠ABD=90°…①
又∵CD为圆的切线，则∠BDC=∠A
又由DA=DC，可得∠A=∠C
∵∠ABD中三角形BCD的外角，
∴∠ABD=∠ADB+∠C=2∠A…②
结合①得：∠DAC=30°
故答案为：30°
由已知中AB为圆O的直径，则∠ADB=90°
∠A+∠ABD=90°…①
又∵CD为圆的切线，则∠BDC=∠A
又由DA=DC，可得∠A=∠C
∵∠ABD中三角形BCD的外角，
∴∠ABD=∠ADB+∠C=2∠A…②
结合①得：∠DAC=30°
故答案为：30°
点评：本题考查的知识点是圆周角定理，弦切角定理，其中根据已知条件结合上述定理，判断出∠DAC=∠C=∠BDC，是解答本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，直三棱柱的一个底面ABC内接于圆O，AB是圆O的直径．
与直线
的夹角大小为
B．（不等式选讲）要使关于x的不等式
在实数