题目内容
(本小题满分14分)已知函数
(1)当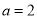 时,求函数
时,求函数 的最值;
的最值;
(2)当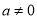 时,过原点分别作曲线
时,过原点分别作曲线 和
和 的切线
的切线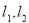 ,已知两切线的斜率互为倒数,证明:
,已知两切线的斜率互为倒数,证明:
(1)最大值为 无最小值 (2)详见解析
无最小值 (2)详见解析
【解析】
试题分析:第(1)问利用导数求函数的单调区间,求解函数的最值;第(2)问背景为指数函数 与对数函数
与对数函数 关于直线
关于直线 对称的特征,得到过原点的切线也关于直线
对称的特征,得到过原点的切线也关于直线 对称,主要考查利用导函数研究曲线的切线及结合方程有解零点存在定理的应该用求参数的问题,得到不等式的证明.
对称,主要考查利用导函数研究曲线的切线及结合方程有解零点存在定理的应该用求参数的问题,得到不等式的证明.
试题解析:(1)当 时,
时, ,定义域为
,定义域为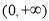 .
.
对 求导,得
求导,得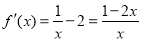 .
.
当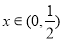 时,
时,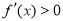 ,当
,当 时,
时, ,即函数
,即函数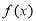 在
在 上单调递增,在
上单调递增,在 上单调递减.
上单调递减.
所以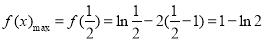 ,没有最小值.
,没有最小值.
(2)设切线 的方程为
的方程为 ,切点为
,切点为 ,则
,则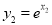 ,
,
 ,所以
,所以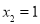 ,
, ,则
,则 .
.
由题意知,切线 的斜率为
的斜率为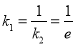 ,
, 的方程为
的方程为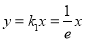 .
.
设 与曲线
与曲线 的切点为
的切点为 ,则
,则 ,
,
所以 ,
,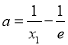 .
.
又因为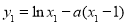 ,消去
,消去 和
和 后,整理得
后,整理得 .
.
令 ,则
,则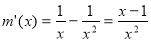 ,
, 在
在 上单调递减,在
上单调递减,在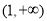 上单调递增.
上单调递增.
若 ,因为
,因为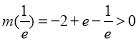 ,
,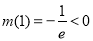 ,所以
,所以 ,
,
而 在
在 上单调递减,所以
上单调递减,所以 .
.
若 ,因为
,因为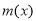 在
在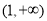 上单调递增,且
上单调递增,且 ,则
,则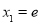 ,
,
所以 (舍去).
(舍去).
综上可知, .
.
考点:导数的几何意义,函数的单调性、最值.

练习册系列答案
相关题目
 ,
, ,则一定有
,则一定有 B.
B. C.
C. D.
D.
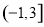 时,
时, 则g(x)= f(x)-|1gx|的零点个数是( )
则g(x)= f(x)-|1gx|的零点个数是( ) ,
, 为正实数,且
为正实数,且 。则
。则 的最小值为 ; 则
的最小值为 ; 则 的最大值为 。
的最大值为 。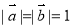 向量
向量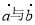 的夹角为120°,且
的夹角为120°,且 ,则实数t的值为( )
,则实数t的值为( ) .-1 B.1 C.-2 D.2
.-1 B.1 C.-2 D.2 和直线
和直线 所围成的平面图形,绕
所围成的平面图形,绕 轴旋转一周所得到的旋转体为
轴旋转一周所得到的旋转体为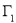 ;由同时满足
;由同时满足 的点
的点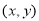 构成的平面图形,绕
构成的平面图形,绕 轴旋转一周所得到的旋转体为
轴旋转一周所得到的旋转体为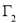 ;根据祖暅原理等知识,通过考察
;根据祖暅原理等知识,通过考察 :
: 的两条渐近线与抛物线
的两条渐近线与抛物线 的准线分别交于
的准线分别交于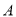 ,
, 两点,
两点,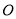 为坐标原点,若双曲线
为坐标原点,若双曲线 的离心率为2,
的离心率为2, 的面积为
的面积为 ,则
,则 B.
B. C.
C.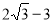 D.
D.
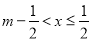 (其中
(其中 为正数),则称
为正数),则称 为离实数
为离实数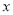 最近的正数,记作
最近的正数,记作 ,即
,即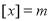
 ,则
,则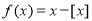 的值域是 ;
的值域是 ;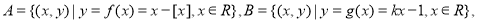 若集合
若集合 的子集恰有4个,则实数
的子集恰有4个,则实数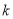 的取值范围为 .
的取值范围为 .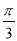 .若
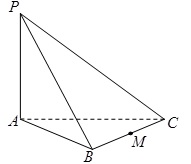
.若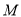 是
是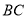 的中点,求:
的中点,求: