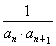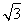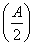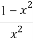题目内容
设正项数列{an}的前n项和是Sn，若{an}和{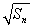
}都是等差数列，且公差相等．
(1)求{an}的通项公式；
(2)若a1， a2，a5恰为等比数列{bn}的前三项，记数列cn＝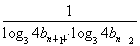
，数列{cn}的前n项和为Tn，求Tn.
（1）
（2）
【解析】(1)设{an}的公差为d，则Sn＝na1＋
，即
＝
，
由是等差数列得到：
，则d＝
且d＝2a1＞0，所以d＝
，
所以a1＝
＝
，an＝
＋(n－1)·
＝.
(2)由b1＝a1＝
，b2＝a2＝
，b3＝a5＝
，得等比数列{bn}的公比q＝3，
所以bn＝
×3n－1，
所以cn＝
＝
，
Tn＝1－
.
练习册系列答案
阅读快车系列答案
相关题目
