题目内容
观察下列导数运算:①(x3)′=3x2;②(sinx)′=cosx;③(ex-(| 1 |
| e |
| 1 |
| e |
分析:由已知中:①(x3)′=3x2;②(sinx)′=cosx;③(ex-(
)x)′=ex+(
)x,…分析其规律,我们可以归纳推断出,奇函数的导函数为偶函数,再结合函数奇偶性的性质,即可得到答案.
| 1 |
| e |
| 1 |
| e |
解答:解:由①中,原函数为偶函数,导函数为奇函数;
②中,原函数为偶函数,导函数为奇函数;
③中,原函数为偶函数,导函数为奇函数;
…
我们可以推断,奇函数的导函数为偶函数.
若定义在R上的函数f(x)满足f(-x)=-f(x),
则函数f(x)为奇函数,
又∵g(x)为f(x)的导函数,
则g(x)偶函数
故g(-x)-g(x)=0
故答案为:0.
②中,原函数为偶函数,导函数为奇函数;
③中,原函数为偶函数,导函数为奇函数;
…
我们可以推断,奇函数的导函数为偶函数.
若定义在R上的函数f(x)满足f(-x)=-f(x),
则函数f(x)为奇函数,
又∵g(x)为f(x)的导函数,
则g(x)偶函数
故g(-x)-g(x)=0
故答案为:0.
点评:本题考查的知识点是归纳推理,及函数奇偶性的性质,其中根据已知中原函数与导函数奇偶性的关系,得到结论是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
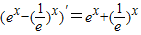 ,由此归纳推理可得:若定义在R上的可导函数f(x)满足f(-x)+f(x)=0,则函数f(x)的导函数g(x)满足g(-x)-g(x)= .
,由此归纳推理可得:若定义在R上的可导函数f(x)满足f(-x)+f(x)=0,则函数f(x)的导函数g(x)满足g(-x)-g(x)= .