题目内容
10.已知锐角△ABC中,满足cos($\frac{π}{4}$+A)cos($\frac{π}{4}$-A)=$\frac{1}{4}$,则A的值等于( )| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{12}$ |
分析 利用诱导公式、倍角公式与和差公式、三角函数的单调性即可得出.
解答 解:∵cos($\frac{π}{4}$+A)cos($\frac{π}{4}$-A)=$\frac{1}{4}$,
∴cos($\frac{π}{4}$+A)sin(A+$\frac{π}{4}$)=$\frac{1}{4}$,
∴$\frac{1}{2}sin(2A+\frac{π}{2})$=$\frac{1}{4}$,
∴cos2A=$\frac{1}{2}$,
∵A∈$(0,\frac{π}{2})$,∴2A∈(0,π).
则2A=$\frac{π}{3}$,
解得A=$\frac{π}{6}$.
故选:C.
点评 本题考查了诱导公式、倍角公式与和差公式、三角函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
18.设l是空间一条直线,α和β是两个不同的平面,则下列结论正确的是( )
| A. | 若l∥α,l∥β,则α∥β | B. | 若α⊥β,l∥α,则l⊥β | C. | 若α⊥β,l⊥α,则l∥β | D. | 若l∥α,l⊥β,则α⊥β |
15.已知a、b、c分别为△ABC三个内角A、B、C所对的边长,∠A=60°,且acosB-bcosA=$\frac{3}{5}$c,则$\frac{2absinC}{{a}^{2}+{b}^{2}-{c}^{2}}$=( )
| A. | -5$\sqrt{3}$ | B. | -4$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 5$\sqrt{3}$ |
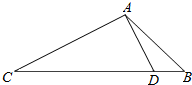 如图△ABC中,已知点D在BC边上,且AD⊥AC,sin∠BAC=$\frac{{2\sqrt{2}}}{3}$,AB=3$\sqrt{2}$,BD=$\sqrt{3}$.
如图△ABC中,已知点D在BC边上,且AD⊥AC,sin∠BAC=$\frac{{2\sqrt{2}}}{3}$,AB=3$\sqrt{2}$,BD=$\sqrt{3}$.