题目内容
已知向量
，其中m，n，θ∈R，若
，则当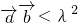
恒成立时实数λ的取值范围是________．
λ＞2或λ＜-2
分析：由已知中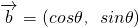
，我们可以得到|
|=1，再由可设
，代入平面向量数量积的坐标运算公式，求出
的取值范围，结合函数恒成立的条件，可以得到一个关于λ的不等式，解不等式即可得到实数λ的取值范围．
解答：∵，，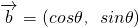
∴设
则=4sinα•cosθ+4cosα•sinθ=4sin（α+θ）∈[-4，4]
若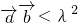恒成立
则λ2＞4
解得λ＞2或λ＜-2
故答案为：λ＞2或λ＜-2．
点评：本题考查的知识点是平面向量数量积的运算、函数恒成立问题、不等式的解法等基础知识，考查运算求解能力，考查转化思想．属于基础题．
分析：由已知中
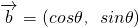，我们可以得到||=1，再由可设，代入平面向量数量积的坐标运算公式，求出的取值范围，结合函数恒成立的条件，可以得到一个关于λ的不等式，解不等式即可得到实数λ的取值范围．解答：∵
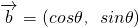，，∴设
则
=4sinα•cosθ+4cosα•sinθ=4sin（α+θ）∈[-4，4]若
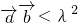恒成立则λ2＞4
解得λ＞2或λ＜-2
故答案为：λ＞2或λ＜-2．
点评：本题考查的知识点是平面向量数量积的运算、函数恒成立问题、不等式的解法等基础知识，考查运算求解能力，考查转化思想．属于基础题．
练习册系列答案
黎明文化寒假作业系列答案
相关题目
，其中m，n，θ∈R，若
，则当
恒成立时实数λ的取值范围是______．
，其中m、n、
。若
，则当
恒成立时，实数
的取值范围是
B．
D．