题目内容

（1+x）（1-x）⁶的二项展开式中，x的系数与x⁵的系数之差为

．

分析：（1+x）（1-x）⁶的展开式中x⁵项由两部分相加得到：①（1+x）中的常数项与（1-x）⁶展开式中的x⁵项 ②（1+x）中的x项与（1-x）⁶展开式中的x⁴项．分别求的系数再相加即可．同理求出x的系数作差即可得到结论．

解答：解：因为：（1+x）（1-x）⁶的展开式中x⁵项由两部分相加得到：
①（1+x）中的常数项与（1-x）⁶展开式中的x⁵项
②（1+x）中的x项与（1-x）⁶展开式中的x⁴项
而：（1-x）⁶的展开式的通项为T_r+1=（-1）^rC₆^rx^r，
∴（1+x）（1-x）⁶的展开式中x⁵的系数等于1×（-1）⁵×C₆⁵+（-1）⁴×C₆⁴=9；
而（1+x）（1-x）⁶的二项展开式中，x的系数由两部分相加得到：①（1+x）中的常数项与（1-x）⁶展开式中的x¹项得系数
②（1+x）中的x项与（1-x）⁶展开式中的常数项的系数．
即1×（-1）¹×C₆¹+（-1）⁰×C₆⁰=-5；
∴x的系数与x⁵的系数之差为：-5-9=-14．
故答案为：-14．

点评：本题考查二项式定理的应用，要注意本题中所求系数应由两部分组成．否则易出错．

练习册系列答案

-1，e-1]时，f（x）＜m恒成立，求实数m的取值范围；
（Ⅲ）若g（x）=x²+x+b，是否存在实数b，使得方程f（x）=g（x）在区间[0，2]上恰有两个相异实数根，若存在，求出b的范围，若不存在说明理由．

探究函数f（x）=x+

，x∈（0，+∞）的最小值，并确定取得最小值时x的值．列表如下：

x	…	0.5	1	1.5	1.7	1.9	2	2.1	2.2	2.3	3	4	5	7	…
y	…	8.5	5	4.17	4.05	4.005	4	4.005	4.02	4.04	4.3	5	5.8	7.57	…

请观察表中值y随x值变化的特点，完成以下的问题．
函数f（x）=x+

（x＞0）在区间（0，2）上递减；
函数f（x）=x+

（x＞0）在区间（0，2）递减．
思考：（直接回答结果，不需证明）
（1）函数f（x）=x+

（x＜0）有没有最值？如果有，请说明是最大值还是最小值，以及取相应最值时x的值．
（2）函数f（x）=ax+

已知函数y＝f(x)满足：；

(1)分别写出x∈[0，1)时y＝f(x)的解析式f₁(x)和x∈[1，2)时y＝f(x)的解析式f₂(x)；并猜想x∈[n，n＋1)，n≥－1，n∈Z时y＝f(x)的解析式f_n+1(x)(用x和n表示)(不必证明)

(2)当(n≥－1，n∈Z)时，y＝f_n+1(x)x∈[n，n＋1)，n≥－1，n∈Z的图象上有点列A_n+1(x，f(x))和点列B_n+1(n＋1，f(n＋1))，线段A_n+1B_n+2与线段B_n+1＋A_n+2的交点C_n+1，求点C_n+1的坐标(a_n+1(x)，b_n+1(x))；

(3)在前面(1)(2)的基础上，请你提出一个点列C_n+1(a_n+1(x)，b_n+1(x))的问题，并进行研究，并写下你研究的过程

设二次函数f（x）=ax²+bx+c（a≠0）满足条件：（1）f（-1+x）=f（-1-x）；（2）函数在y轴上的截距为1，且f（x+1）-f（x）=x+ $数学公式$ ．
（1）求f（x）的解析式；
（2）若x∈[t，t+1]，f（x）的最小值为h（t），请写出h（t）的表达式；
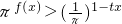（3）若不等式 $数学公式$ 在t∈[-2，2]时恒成立，求实数x的取值范围．

设函数f（x）=（1+x）²-ln（1+x）²+2．
（1）求函数f（x）的单调增区间；
（2）若不等式f（x）＞m在

恒成立，求实数m的取值范围．
（3）若对任意的a∈（1，2），总存在x∈[1，2]，使不等式

成立，求实数m的取值范围．

试题分类