题目内容
平行于直线3x+4y-12=0,且与它的距离是7的直线的方程为
3x+4y+23=0或3x+4y-47=0
3x+4y+23=0或3x+4y-47=0
.分析:设所求的直线方程为3x+4y+c=0,由于两条平行线间的距离为7,利用两条平行线之间的距离公式可得
=7,解出即可.
| |-12-c| | ||
|
解答:解:设所求的直线方程为3x+4y+c=0,
∵两条平行线间的距离为7,
∴
=7,化为|12+c|=35,
解得c=23或-47,
故所求的直线方程为3x+4y+23=0或3x+4y-47=0.
故答案为3x+4y+23=0或3x+4y-47=0.
∵两条平行线间的距离为7,
∴
| |-12-c| | ||
|
解得c=23或-47,
故所求的直线方程为3x+4y+23=0或3x+4y-47=0.
故答案为3x+4y+23=0或3x+4y-47=0.
点评:本题考查了两条平行线之间的距离公式,属于基础题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
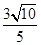 的直线方程.
的直线方程.