题目内容
设0<θ<(1)求θ的取值范围;
(2)证明这4个交点共圆,并求圆半径的取值范围.
思路解析:由经验知,要求θ的三角函数范围,想到两曲线有4个交点,则θ满足的方程组有4个解,问题(1)获解;要证四点共圆,由圆的定义可知,只需证明这4个点到某定点的距离相等即可. (1)解:设交点坐标为(x,y), 则其满足方程组 ∴ 又∵0<θ< ∴θ的取值范围是(0, (2)证明:由(1)得4个交点的坐标满足方程x2+y2=2cosθ(0<θ< 即 ∴四个交点到原点的距离均等于 ∴四个交点共圆,半径r= ∵0<θ< 方法归纳 解决多点共圆问题,只需证明这些点到某定点的距离均相等即可.定点是圆心,定距离是圆的半径.
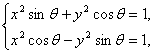 即
即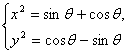 有4个解,则x2>0,y2>0.
有4个解,则x2>0,y2>0.![]() 即
即![]()
![]() ,∴
,∴![]()
![]() ).
).![]() ),
),![]() =
=![]() .
.![]() .
.![]() .
.![]() ,∴
,∴![]() <r<
<r<![]() .∴圆半径的取值范围是(
.∴圆半径的取值范围是(![]() ,
,![]() ).
). 练习册系列答案
练习册系列答案
2点备考案系列答案
68所名校图书全国著名重点中学3年招生试卷及预测试题精选系列答案
53中考真题卷系列答案
A级口算系列答案
A加优化作业本系列答案
BBS试卷精编系列答案
LeoLiu中学英语系列答案
N版英语综合技能测试系列答案
PK中考系列答案
X新目标英语系列答案
相关题目
设直线x+ky-1=0被圆O:x2+y2=2所截弦的中点的轨迹为M,则曲线M与直线x-y-1=0位置关系为( )
| A、相离 | B、相切 | C、相交 | D、不确定 |
 (2013•杭州模拟)如图,由半圆x2+y2=1(y≤0)和部分抛物线y=a(x2-1)(y≥0,a>0)合成的曲线C称为“羽毛球形线”,且曲线C经过点(2,3).
(2013•杭州模拟)如图,由半圆x2+y2=1(y≤0)和部分抛物线y=a(x2-1)(y≥0,a>0)合成的曲线C称为“羽毛球形线”,且曲线C经过点(2,3).