题目内容
若b>a>3,f(x)= ,则下列各结论中正确的是
,则下列各结论中正确的是
- A.

- B.

- C.f(
 )<f(
)<f( )<f(a)
)<f(a) - D.f(b)<f(
 )<f(
)<f( )
)
D
分析:对f(x)= 进行求导,求出其单调区间,再根据均值不等式判断
进行求导,求出其单调区间,再根据均值不等式判断 ,ab,a,
,ab,a, 的大小,从而判断其函数值的大小;
的大小,从而判断其函数值的大小;
解答:∵f(x)= ,
,
∴f′(x)= ,令f′(x)=0,解得x=e,
,令f′(x)=0,解得x=e,
当x≥e时,f′(x)<0,为减函数,当0<x<e时,f′(x)>0,为增函数,
∵b>a>3>e,
∴ab>b> >
> >a>e,
>a>e,
∴f(a)>f( )>f(
)>f( )>f(b)>f(ab),
)>f(b)>f(ab),
故选D.
点评:此题考查利用导数研究函数的单调性,解题的关键是要正确求出导数,此题还涉及不等式 ,是一道不错的题.
,是一道不错的题.
分析:对f(x)=
 进行求导,求出其单调区间,再根据均值不等式判断
进行求导,求出其单调区间,再根据均值不等式判断 ,ab,a,
,ab,a, 的大小,从而判断其函数值的大小;
的大小,从而判断其函数值的大小;解答:∵f(x)=
 ,
,∴f′(x)=
 ,令f′(x)=0,解得x=e,
,令f′(x)=0,解得x=e,当x≥e时,f′(x)<0,为减函数,当0<x<e时,f′(x)>0,为增函数,
∵b>a>3>e,
∴ab>b>
 >
> >a>e,
>a>e,∴f(a)>f(
 )>f(
)>f( )>f(b)>f(ab),
)>f(b)>f(ab),故选D.
点评:此题考查利用导数研究函数的单调性,解题的关键是要正确求出导数,此题还涉及不等式
 ,是一道不错的题.
,是一道不错的题. 
练习册系列答案
相关题目
 ,则下列各结论中正确的是( )
,则下列各结论中正确的是( )

 )<f(
)<f( )<f(a)
)<f(a) )<f(
)<f( )
) ,则下列各结论中正确的是( )
,则下列各结论中正确的是( )

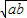 )<f(
)<f( )<f(a)
)<f(a) )<f(
)<f( )
) ,则下列各结论中正确的是( )
,则下列各结论中正确的是( )

 )<f(
)<f( )<f(a)
)<f(a) )<f(
)<f( )
) ,则下列各结论中正确的是( )
,则下列各结论中正确的是( )

 )<f(
)<f( )<f(a)
)<f(a) )<f(
)<f( )
)