题目内容
已知点 ,椭圆E:
,椭圆E: 的离心率为
的离心率为 ;F是椭圆E的右焦点,直线AF的斜率为
;F是椭圆E的右焦点,直线AF的斜率为 ,O为坐标原点;
,O为坐标原点;
(I)求E的方程;
(II)设过点A的动直线 与E 相交于P,Q两点,当
与E 相交于P,Q两点,当 的面积最大时,求
的面积最大时,求 的直线方程.
的直线方程.
【解析】(I)设右焦点 ,由条件知,
,由条件知, ,得
,得 .
.
又 ,所以
,所以 ,
,
 .故椭圆
.故椭圆 的方程为
的方程为 .
.
(II)当 轴时不合题意,故设直线
轴时不合题意,故设直线
 ,
, .
.
将 代入
代入 得
得 .当
.当 ,
,
即 时,.从而
时,.从而 .又点
.又点 到直线
到直线 的距离
的距离
 ,所以
,所以 的面积
的面积 .设
.设 ,则
,则 ,
, .因为
.因为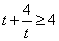 ,当且仅当
,当且仅当 时,
时, 时取等号,且满足
时取等号,且满足 .所以,当
.所以,当 的面积最大时,
的面积最大时, 的方程为
的方程为 或
或 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,则
,则
 ,椭圆
,椭圆 的方程为
的方程为 ,双曲线
,双曲线 的方程为
的方程为 ,
, B.
B. C.
C. D.
D.
 ,
, ,且
,且  是
是 的充分不必要条件,
的充分不必要条件, 的取值范围;
的取值范围; 的值域是( )
的值域是( ) (B)
(B) (C)
(C) (D)
(D)
 ,若
,若 在
在 上恒成立,则实数
上恒成立,则实数 的取值范围
的取值范围 或
或 (B)
(B) (C)
(C) (D)
(D) 或
或 .若事件A与事件B是互斥事件,则
.若事件A与事件B是互斥事件,则 ;
;  .若事件A与事件B满足条件:
.若事件A与事件B满足条件: ,则事件A与事件B是 对立事件;
,则事件A与事件B是 对立事件; .一个人打靶时连续射击两次,则事件 “至少有一次中靶”与事件 “至多有一次中靶”是对立事件;
.一个人打靶时连续射击两次,则事件 “至少有一次中靶”与事件 “至多有一次中靶”是对立事件; .把红、橙、黄、绿4张纸牌随机分给甲、乙、丙、丁 4人,每人分得1张,则事件“甲分得红牌”与事件“乙分得红牌”是互斥事件.
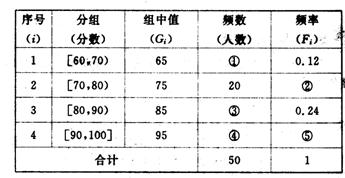
.把红、橙、黄、绿4张纸牌随机分给甲、乙、丙、丁 4人,每人分得1张,则事件“甲分得红牌”与事件“乙分得红牌”是互斥事件.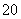 的样本.已知乙层中每个个体被抽到的概率都为
的样本.已知乙层中每个个体被抽到的概率都为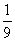 ,则总体中的个体数为 .
,则总体中的个体数为 .