题目内容
已知函数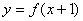 的图象关于点
的图象关于点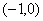 对称,且当
对称,且当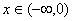 时,
时,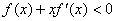 成立(其中
成立(其中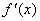 是
是 的导函数),若
的导函数),若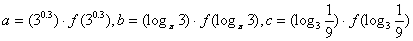 ,则a,b,c的大小关系为( )
,则a,b,c的大小关系为( )
| A.a > c >b | B.c>a>b | C.c> b > a | D.b >a> c |
B
解析试题分析:∵当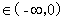 时不等式
时不等式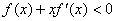 成立
成立
即: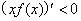 ,∴
,∴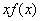 在
在 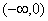 上是减函数.
上是减函数.
又∵函数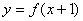 的图象关于点
的图象关于点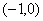 对称,∴函数
对称,∴函数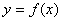 的图象关于点
的图象关于点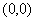 对称,
对称,
∴函数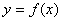 是定义在R上的奇函数 ∴
是定义在R上的奇函数 ∴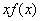 是定义在R上的偶函数
是定义在R上的偶函数
∴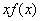 在
在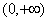 上是增函数. 又∵
上是增函数. 又∵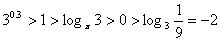 ,
,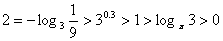 ,
,
所以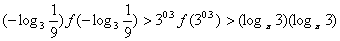
即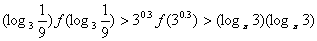 ,故
,故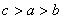 .
.
考点:不等关系与不等式;奇偶性与单调性的综合.
点评:本题主要考查了函数的奇偶性以及函数的单调性,同时考查了分析问题的能力和运算求解的能力,属于中档题.

练习册系列答案
相关题目
设函数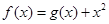 ,曲线
,曲线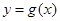 在点
在点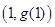 处的切线方程为
处的切线方程为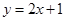 ,则曲线
,则曲线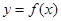 在点
在点 处切线的斜率为
处切线的斜率为
| A.4 | B.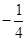 | C. | D.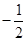 |
设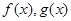 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当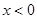 时,
时, ,且
,且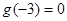 ,则
,则 的解集是( )
的解集是( )
| A.(-3,0)∪(3,+∞) | B.(-3,0)∪(0,3) |
| C.(-∞,-3)∪(3,+∞) | D. (-∞,-3)∪(0,3) |
函数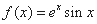 的图象在点
的图象在点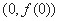 处的切线的倾斜角为
处的切线的倾斜角为
A. | B.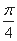 | C.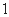 | D.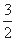 |
直线 与曲线
与曲线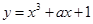 相切于点(2,3),则
相切于点(2,3),则 的值为( )
的值为( )
| A.-3 | B.9 | C.-15 | D.-7 |
若曲线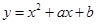 在点
在点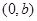 处的切线方程是
处的切线方程是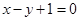 ,则( )
,则( )
A.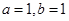 | B.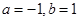 |
C.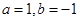 | D.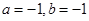 |
设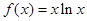 ,若
,若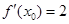 ,则
,则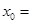 ( )
( )
A.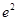 | B.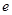 | C.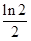 | D.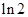 |
设曲线 在点(1,1)处的切线与x轴的交点的横坐标为
在点(1,1)处的切线与x轴的交点的横坐标为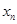 ,则
,则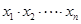 的值为( )
的值为( )
A.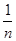 | B.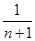 | C.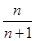 | D.1 |
已知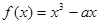 在(-∞,-1)上单调递增,则
在(-∞,-1)上单调递增,则 的取值范围是( )
的取值范围是( )
A. <3 <3 | B.  3 3 | C. >3 >3 | D. 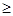 3 3 |