题目内容
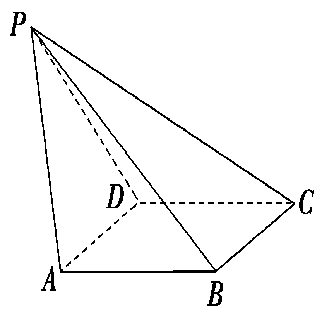
(本小题满分12分)如图,在四棱锥 中,平面PAD⊥平面 ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点
中,平面PAD⊥平面 ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点
求证:(1)直线EF∥平面PCD;
(2)平面BEF⊥平面PAD
(1)见解析;(2)见解析。
解析试题分析:(1)在△PAD中,因为E、F分别为AP,AD的中点,所以EF//PD.
又因为EF 平面PCD,PD
平面PCD,PD 平面PCD,所以直线EF//平面PCD.
平面PCD,所以直线EF//平面PCD.
(2)连结DB,因为AB=AD,∠BAD=60°,
所以△ABD为正三角形,因为F是AD的中点,所以BF⊥AD.因为平面PAD⊥平面ABCD,
BF 平面ABCD,平面PAD
平面ABCD,平面PAD 平面ABCD=AD,所以BF⊥平面PAD。又因为BF
平面ABCD=AD,所以BF⊥平面PAD。又因为BF 平面BEF,所以平面BEF⊥平面PAD。
平面BEF,所以平面BEF⊥平面PAD。
考点:面面垂直的性质定理;面面垂直的判定定理;线面垂直的判定定理;中位线的性质。
点评:本题是中档题,考查直线与平面平行,平面与平面的垂直的证明方法,我们一定要熟练掌握性质定理和判定定理,同时本题也考查了空间想象能力,逻辑推理能力,属于常考题型。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,E、F分别是AB、PD的中点.
,E、F分别是AB、PD的中点.
 平面PCD;
平面PCD;
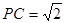 ,求四面体PABC的体积.
,求四面体PABC的体积. 分别是
分别是 中点)
中点)
 平面
平面 ;
; 的体积.
的体积. 中
中 ,
, 为
为 中点.
中点.
 ;
; 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面 若存在,求
若存在,求 的长;若不存在,说明理由.
的长;若不存在,说明理由. 
 上找一点M,在AD上找点N,使平面MED//平面BFN,说明理由;并求出
上找一点M,在AD上找点N,使平面MED//平面BFN,说明理由;并求出 的值
的值
 A1D;
A1D; 。
。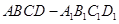 中,
中,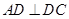 ,
,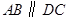 ,
,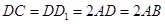
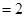 .
.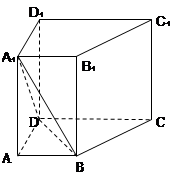
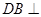 平面
平面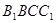 ;
; 是
是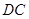 上一点,试确定
上一点,试确定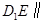 平面
平面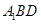 ,并说明理由.
,并说明理由.