题目内容
已知集合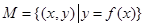 ,若对于任意实数对
,若对于任意实数对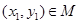 ,存在
,存在 ,使得
,使得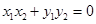 成立,则称集合
成立,则称集合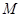 为“正交点集”,给出下列集合:
为“正交点集”,给出下列集合:
①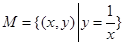 ;②
;②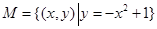 ;③
;③ ;
;
④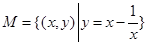 ;⑤
;⑤ .
.
则满足条件的“正交集合”有:_________________________(写出所有满足条件的集合的序号)
②③⑤
解析试题分析:①中取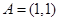 ,则不存在
,则不存在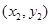 使
使 且
且 ;
;
④中取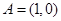 ,则不存在
,则不存在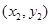 使
使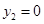 且
且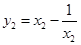 ,
,
所以②③⑤正确.
考点:新定义题.

练习册系列答案
相关题目
设集合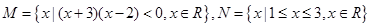 ,则
,则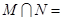
A.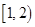 | B. | C.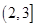 | D. |
设非空集合P、Q满足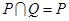 ,则
,则
A. x x Q,有x Q,有x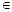 P P | B.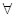 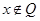 ,有 ,有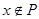 |
C.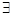 x0 x0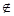 Q,使得x0 Q,使得x0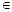 P P | D.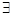 x0 x0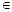 P,使得x0 P,使得x0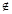 Q Q |
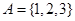 ,集合
,集合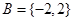 ,则
,则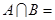 .
.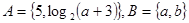 ,若
,若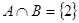 ,则
,则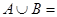 .
.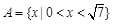 ,则
,则 Z= .
Z= .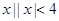 },B={
},B={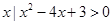 },则集合{
},则集合{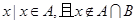 }=
}= 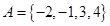 ,
,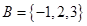 ,则
,则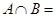 .
.