题目内容
已知函数f(x)=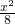 -lnx,x∈[1,3],
-lnx,x∈[1,3],
(1)求f(x)的最大值与最小值;
(2)若f(x)<4-at于任意的x∈[1,3],t∈[0,2]恒成立,求实数a的取值范围.
解:(1)因为函数f(x)=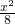 -lnx,
-lnx,
所以f′(x)=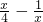 ,令f′(x)=0得x=±2,
,令f′(x)=0得x=±2,
因为x∈[1,3],
当1<x<2时 f′(x)<0;当2<x<3时,f′(x)>0;
∴f(x)在(1,2)上单调减函数,在(2,3)上单调增函数,
∴f(x)在x=2处取得极小值f(2)= -ln2;
-ln2;
又f(1)= ,f(3)=
,f(3)=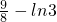 ,
,
∵ln3>1∴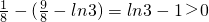
∴f(1)>f(3),
∴x=1时 f(x)的最大值为 ,
,
x=2时函数取得最小值为 -ln2.
-ln2.
(2)由(1)知当x∈[1,3]时,f(x)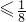 ,
,
故对任意x∈[1,3],f(x)<4-at恒成立,
只要4-at> 对任意t∈[0,2]恒成立,即at
对任意t∈[0,2]恒成立,即at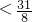 恒成立
恒成立
记 g(t)=at,t∈[0,2]
∴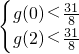 ,解得a
,解得a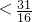 ,
,
∴实数a的取值范围是(-∞,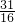 ).
).
分析:(1)直接求出函数的导数,通过导数为0,求出函数的极值点,判断函数的单调性,利用最值定理求出f(x)的最大值与最小值;
(2)利用(1)的结论,f(x)<4-at于任意的x∈[1,3],t∈[0,2]恒成立,转化为4-at> 对任意t∈[0,2]恒成立,通过
对任意t∈[0,2]恒成立,通过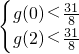 ,求实数a的取值范围.
,求实数a的取值范围.
点评:本题考查函数与导数的关系,函数的单调性的应用,考查函数的导数在闭区间上的最值的求法,考查计算能力,恒成立问题的应用,考查转化思想,计算能力.
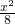 -lnx,
-lnx,所以f′(x)=
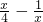 ,令f′(x)=0得x=±2,
,令f′(x)=0得x=±2,因为x∈[1,3],
当1<x<2时 f′(x)<0;当2<x<3时,f′(x)>0;
∴f(x)在(1,2)上单调减函数,在(2,3)上单调增函数,
∴f(x)在x=2处取得极小值f(2)=
 -ln2;
-ln2;又f(1)=
 ,f(3)=
,f(3)=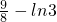 ,
,∵ln3>1∴
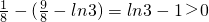
∴f(1)>f(3),
∴x=1时 f(x)的最大值为
 ,
,x=2时函数取得最小值为
 -ln2.
-ln2.(2)由(1)知当x∈[1,3]时,f(x)
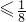 ,
,故对任意x∈[1,3],f(x)<4-at恒成立,
只要4-at>
 对任意t∈[0,2]恒成立,即at
对任意t∈[0,2]恒成立,即at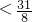 恒成立
恒成立记 g(t)=at,t∈[0,2]
∴
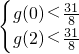 ,解得a
,解得a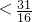 ,
,∴实数a的取值范围是(-∞,
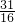 ).
).分析:(1)直接求出函数的导数,通过导数为0,求出函数的极值点,判断函数的单调性,利用最值定理求出f(x)的最大值与最小值;
(2)利用(1)的结论,f(x)<4-at于任意的x∈[1,3],t∈[0,2]恒成立,转化为4-at>
 对任意t∈[0,2]恒成立,通过
对任意t∈[0,2]恒成立,通过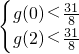 ,求实数a的取值范围.
,求实数a的取值范围.点评:本题考查函数与导数的关系,函数的单调性的应用,考查函数的导数在闭区间上的最值的求法,考查计算能力,恒成立问题的应用,考查转化思想,计算能力.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|