Question

已知三次波函数f ( x )的导函数为f′( x )，f′( 1 ) = 0 , f′(2 ) = 3 , f′( 3 ) = 12 .

（1）求f ( x ) f ( 0 )的表达式；

（2）若对任意的x∈[ 1 , 4 ]，都有成立，求的取值范围。

Answer 1

解：（1）设f ( x ) = ax³ + bx² + cx + d . 则f′( x ) = 3ax² + 2bx + c ,

于是有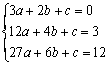

∴      故f ( x ) f ( 0 ) = x³ 3x² + 3x

（2）由（1）得f′( x ) = 3x² 6x + 3 . 对任意的x∈[ 1 , 4 ], f ( x )＞f′( x )

等价于f ( x ) f′( x ) = x³ 6x² + 9x + f ( 0 ) 3 ＞0，

令F ( x ) = x³ + 6x² 9x + 3 ,

则f ( 0 )＞F ( x ) = x³ + 6x² 9x + 3

因为F′( x ) = 3x² + 12x 9 当x∈时，F′( x )＜0；

当x = 1 或3时，F′( x ) = 0

当x∈( 1 , 3 )时，F′( x )＞0

当x∈时，F′( x )＜0

又F ( 1 )＞F ( 3 )

所以F ( x )在[ 1 ，4]上的最大值为F ( 1 ) = 19

故f ( 0 )的取值范围是（19，+∞）