题目内容
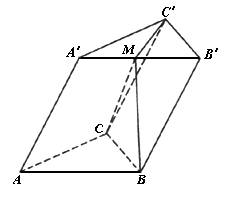
如图三棱柱ABC-A1B1C1中，E，F分别是AB、AC的中点，平面EFC1B1将三棱柱分成体积为V1，V2（左为V1，右为V2）两部分，则V1：V2=
- A.7：5
- B.4：3
- C.3：1
- D.2：1
A
分析：设AEF面积为s1，ABC和A1B1C1的面积为s，三棱柱高位h；VAEF-A1B1C1=V1；VBCFE-B1C1=V2；总体积为：V，根据棱台体积公式求V1；V2=V-V1以及面积关系，求出体积之比．
解答：由题：设AEF面积为s1，ABC和A1B1C1的面积为s，三棱柱高位h；VAEF-A1B1C1=V1；
VBCFE-B1C1=V2；总体积为：V
计算体积：
V1=
h（s1+s+
）①
V=sh ②
V2=V-V1③
由题意可知，s1=
④
根据①②③④解方程可得：V1=
sh，V2=
sh；则 
故选A．
点评：本题考查的知识点是棱柱的体积，棱台的体积，组合体的体积，其中分析出面EB'C'F将三棱柱分成一个棱台（体积为V1）和一个不规则几何体，（体积为V2），是解答本题的关键．
分析：设AEF面积为s1，ABC和A1B1C1的面积为s，三棱柱高位h；VAEF-A1B1C1=V1；VBCFE-B1C1=V2；总体积为：V，根据棱台体积公式求V1；V2=V-V1以及面积关系，求出体积之比．
解答：由题：设AEF面积为s1，ABC和A1B1C1的面积为s，三棱柱高位h；VAEF-A1B1C1=V1；
VBCFE-B1C1=V2；总体积为：V
计算体积：
V1=
h（s1+s+）①V=sh ②
V2=V-V1③
由题意可知，s1=
④根据①②③④解方程可得：V1=
sh，V2=sh；则 故选A．
点评：本题考查的知识点是棱柱的体积，棱台的体积，组合体的体积，其中分析出面EB'C'F将三棱柱分成一个棱台（体积为V1）和一个不规则几何体，（体积为V2），是解答本题的关键．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
如图三棱柱ABC-A1B1C1中，侧棱BB1与底面成60．角，AQ⊥底面A1B1C1于Q，AP⊥侧面BCC1B1于P，且A1Q⊥B1C1，AB=AC，AQ=3，AP=2则顶点A到棱B1C1的距离是
如图三棱柱ABC-A1B1C1中，E，F分别是AB、AC的中点，平面EFC1B1将三棱柱分成体积为V1，V2（左为V1，右为V2）两部分，则V1：V2=（ ）| A、7：5 | B、4：3 | C、3：1 | D、2：1 |
某人有4种颜色的灯泡（每种颜色的灯泡足够多），要在如图三棱柱ABC-A1B1C1的六个顶点上各安装一个灯泡，要求同一条线段的两端的灯泡颜色不同，则每种颜色的灯泡至少用一个的安装方法共有（ ）
