题目内容

求证：
cosα
1+sinα
-
sinα
1+cosα
=
2(cosα-sinα)
1+sinα+cosα
．
分析：从等式左边入手，乘上
1+sina+cosa
1+sina+cosa
，进行分子的多项式的展开，化简，约分，证出右边即可．
解答：证明：左边=
1+sina+cosa
1+sina+cosa
(
cosa
1+sina
-
sina
1+cosa
)
=
1
1+sina+cosa
[
(1+sina+cosa)cosa
1+sina
-
(1+cosa+sina)sina
1+cosa
]
=
1
1+sina+cosa
[cosa+
cos2a
1+sina
-sina-
sin2a
1+cosa
]
=
1
1+sina+cosa
(cosa+1-sina-sina-1+cosa)
=
2(cosa-sina)
1+sina+cosa
=右边．
故原式成立．
点评：本题考查恒等式的证明，一般情况下“左?右”；“右?左”；或者借助中间量来证明．大多借助公式的灵活运用．
练习册系列答案
相关题目
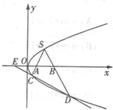精英家教网如图，S（1，1）是抛物线为y2=2px（p＞0）上的一点，弦SC，SD分别交x小轴于A，B两点，且SA=SB．
（I）求证：直线CD的斜率为定值；
（Ⅱ）延长DC交x轴于点E，若
EC
=
1
3
ED
，求cos∠CSD的值．
定义非零向量
OM
=(a，b)的“相伴函数”为f（x）=asinx+bcosx（x∈R），向量
OM
=(a，b)称为函数f（x）=asinx+bcosx的“相伴向量”（其中O为坐标原点）．记平面内所有向量的“相伴函数”构成的集合为S．
（1）设h（x）=cos（x+
π
6
）-2cos（x+a）（a∈R），求证：h（x）∈S；
（2）求（1）中函数h（x）的“相伴向量”模的取值范围；
（3）已知点M（a，b）（b≠0）满足：(a-
3
)2+(b-1)2=1上一点，向量
OM
的“相伴函数”f（x）在x=x0处取得最大值．当点M运动时，求tan2x0的取值范围．
（2012•上海）定义向量
OM
=（a，b）的“相伴函数”为f（x）=asinx+bcosx，函数f（x）=asinx+bcosx的“相伴向量”为
OM
=（a，b）（其中O为坐标原点）．记平面内所有向量的“相伴函数”构成的集合为S．
（1）设g（x）=3sin（x+
π
2
）+4sinx，求证：g（x）∈S；
（2）已知h（x）=cos（x+α）+2cosx，且h（x）∈S，求其“相伴向量”的模；
（3）已知M（a，b）（b≠0）为圆C：（x-2）2+y2=1上一点，向量
OM
的“相伴函数”f（x）在x=x0处取得最大值．当点M在圆C上运动时，求tan2x0的取值范围．
定义向量=（a，b）的“相伴函数”为f（x）=asinx+bcosx，函数f（x）=asinx+bcosx的“相伴向量”为=（a，b）（其中O为坐标原点）．记平面内所有向量的“相伴函数”构成的集合为S．
（1）设g（x）=3sin（x+）+4sinx，求证：g（x）∈S；
（2）已知h（x）=cos（x+α）+2cosx，且h（x）∈S，求其“相伴向量”的模；
（3）已知M（a，b）（b≠0）为圆C：（x-2）2+y2=1上一点，向量的“相伴函数”f（x）在x=x处取得最大值．当点M在圆C上运动时，求tan2x的取值范围．
如图，S（1，1）是抛物线为y2=2px（p＞0）上的一点，弦SC，SD分别交x小轴于A，B两点，且SA=SB．
（I）求证：直线CD的斜率为定值；
（Ⅱ）延长DC交x轴于点E，若，求cos∠CSD的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网