题目内容
若向量 ,
, 满足
满足 ,
, ,且
,且 ,则
,则 与
与 的夹角为( )
的夹角为( )
A. | B. | C. | D. |
C
解析试题分析:因为 ,所以
,所以 ,即
,即 ,解得
,解得 ,所以
,所以 ,所以
,所以 与
与 的夹角为
的夹角为 .
.
考点:平面向量的数量积和夹角

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
已知向量a,b,c满足 ,
, ,则
,则 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
如图,菱形 的边长为
的边长为 ,
, ,
, 为
为 的中点,若
的中点,若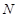 为菱形内任意一点(含边界),则
为菱形内任意一点(含边界),则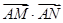 的最大值为( )
的最大值为( )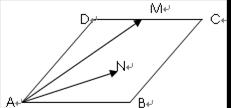
A. | B. | C.9 | D.6 |
如右图所示, 是圆
是圆 上的三点,
上的三点, 的延长线与线段
的延长线与线段 交于圆内一点
交于圆内一点 ,若
,若 ,则( )
,则( )
A. | B. |
C. | D. |
已知 ,则
,则 ( )
( )
A. | B.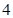 | C. | D. |
已知平面向量 ,
, ,满足
,满足 ,
, ,
, ,则
,则 =( )
=( )
| A.2 | B.3 | C.4 | D.6 |
若向量a=(1,2),b=(1,-1),则2a+b与a-b的夹角等于( )
A.- 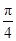 | B.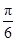 | C.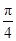 | D. |
 ,若对于任意
,若对于任意 ,存在
,存在 ,使得
,使得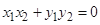 成立,则称集合
成立,则称集合 是“理想集合”,则下列集合是“理想集合”的是( )
是“理想集合”,则下列集合是“理想集合”的是( )
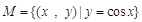

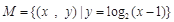
 ,它们的夹角是60°,
,它们的夹角是60°, 与
与 、
、 向量的夹角都为
向量的夹角都为 ,且|
,且| ,若
,若 ,则
,则 值为( )
值为( )
