题目内容
10.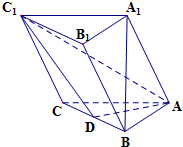 如图,在三棱柱ABC-A1B1C1中,D为棱BC的中点,AB⊥BC,BC⊥BB1,AB=A1B=1,BB1=$\sqrt{2}$.求证:
如图,在三棱柱ABC-A1B1C1中,D为棱BC的中点,AB⊥BC,BC⊥BB1,AB=A1B=1,BB1=$\sqrt{2}$.求证:(1)A1B⊥平面ABC;
(2)A1B∥平面AC1D.
分析 (1)欲证明A1B⊥平面ABC,只需证得A1B垂直于平面ABC内的两条相交线即可;
(2)连接A1C交AC1与点E,连接DE,构建三角形的中位线,利用三角形中位线定理推知DE∥A1B,则根据“如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行”证得结论.
解答 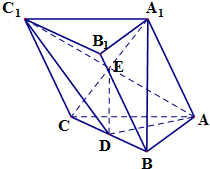 证明:(1)因为AB⊥BC,BC⊥BB1,AB∩BB1=B,AB、BB1?平面ABB1,
证明:(1)因为AB⊥BC,BC⊥BB1,AB∩BB1=B,AB、BB1?平面ABB1,
所以BC⊥平面ABB1,
又AB1?平面ABB1,
所以AB1⊥BC;
又因为$AB={A_1}B=1,B{B_1}=\sqrt{2}=A{A_1}$,得
$A{A_1}^2=A{B^2}+{A_1}{B^2}$,
所以A1B⊥AB.
又AB、BC?平面ABC,AB∩BC=B,所以A1B⊥平面ABC;
(2)连接A1C交AC1与点E,连接DE,在△A1BC中,D、E分别为BC、A1C的中点,
所以DE∥A1B,
又A1B?平面AC1D,DE?平面AC1D,
所以A1B∥平面AC1D.
点评 本题考查了直线与平面平行的判定,直线与平面垂直的判定.熟练掌握线面面面平行于垂直的判定定理及其性质定理、勾股定理及其逆定理、三角形的中位线定理等是解题的关键.

练习册系列答案
相关题目
4.半径为1的球的表面积为( )
| A. | 1 | B. | 2π | C. | 3π | D. | 4π |
1.甲、乙两人独立地解决同一个问题,甲能解决这个问题的概率是P1,乙能解决这个问题的概率是P2,那么至少有1人解决这个问题的概率是( )
| A. | P1+P2 | B. | P1•P2 | C. | 1-P1•P2 | D. | 1-(1-P1)(1-P2) |
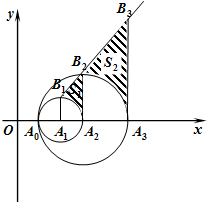 如图,在平面直角坐标系xOy中,设a1=2,有一组圆心在x轴正半轴上的圆An(n=1,2,…)与x轴的交点分别为A0(1,0)和An+1(an+1,0).过圆心An作垂直于x轴的直线ln,在第一象限与圆An交于点Bn(an,bn).
如图,在平面直角坐标系xOy中,设a1=2,有一组圆心在x轴正半轴上的圆An(n=1,2,…)与x轴的交点分别为A0(1,0)和An+1(an+1,0).过圆心An作垂直于x轴的直线ln,在第一象限与圆An交于点Bn(an,bn).