题目内容
在Rt△ABC中，∠A=90°,AB=6,AC=8,PA为平面ABC的斜线，且∠PAB=∠PAC=60°.求PA与平面ABC所成的角.
解析:如图,设P在平面ABC上的射影为P′.
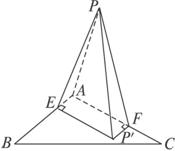
作P′F⊥AC于F,P′E⊥AB于E，连结PF,PE.
∵PP′⊥平面ABC，∴PP′⊥AE.
又AE⊥P′E,PP′∩P′E=P′,且PP′、P′E
面PP′E,
∴AE⊥平面PP′E.故AE⊥PE.
同理,AF⊥PF.在Rt△PAE与Rt△PAF中，PA公共，∠PAE=∠PAF=60°.
故Rt△PAE≌Rt△PAF.∴AE=AF.
设AE=AF=a,故AP=
故AP′=
.又PP′⊥平面ABC，
∴∠PAP′是PA与平面ABC所成的角,
且cos∠PAP′=
=
,
∴∠PAP′=45°,
即PA与平面ABC所成的角为45°.
练习册系列答案
特高级教师点拨系列答案
相关题目
如图所示，在Rt△ABC中，∠ACB=90°，CD⊥AB于D，且AD：BD=9：4，则AC：BC=
（几何证明选讲选做题）