题目内容
已知函数f(x)=exsinx.(1)求函数f(x)的单调区间;
(2)如果对于任意的x∈[0,
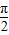 ],f(x)≥kx总成立,求实数k的取值范围;
],f(x)≥kx总成立,求实数k的取值范围;(3)设函数F(x)=f(x)+excosx,x∈[
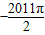 ,
,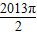 ].过点M(
].过点M(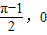 )作函数F(x)图象的所有切线,令各切点的横坐标构成数列{xn},求数列{xn}的所有项之和S的值.
)作函数F(x)图象的所有切线,令各切点的横坐标构成数列{xn},求数列{xn}的所有项之和S的值.
【答案】分析:(1)求出函数的导函数,由导函数大于0求其增区间,导函数小于0求其减区间;
(2)构造辅助函数g(x)=f(x)-kx,把问题转化为求x∈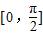 时g(x)min≥0,然后对k的值进行分类讨论,求k在不同取值范围内时的g(x)的最小值,由最小值大于等于0得到k的取值范围;
时g(x)min≥0,然后对k的值进行分类讨论,求k在不同取值范围内时的g(x)的最小值,由最小值大于等于0得到k的取值范围;
(3)把f(x)的解析式代入F(x)=f(x)+excosx,求出函数F(x)的导函数,设出切点坐标,求出函数在切点处的导数,由点斜式写出切线方程,把M的坐标代入切线方程,得到关于切点横坐标的三角方程,利用函数图象交点分析得到切点的横坐标关于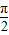 对称成对出现,最后由给出的自变量的范围得到数列{xn}的所有项之和S的值.
对称成对出现,最后由给出的自变量的范围得到数列{xn}的所有项之和S的值.
解答:解:(1)由于f(x)=exsinx.所以
f′(x)=exsinx+excosx=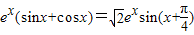 .
.
当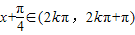 ,即
,即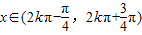 时,f′(x)>0;
时,f′(x)>0;
当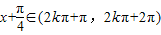 ,即
,即 时,f′(x)<0.
时,f′(x)<0.
所以f(x)的单调递增区间为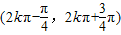 (k∈Z),
(k∈Z),
单调递减区间为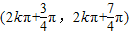 (k∈Z).
(k∈Z).
(2)令g(x)=f(x)-kx=exsinx-kx,要使f(x)≥kx总成立,只需在x∈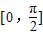 时g(x)min≥0.
时g(x)min≥0.
对g(x)求导得g′(x)=ex(sinx+cosx)-k,
令h(x)=ex(sinx+cosx),则h′(x)=2excosx>0,(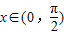 )
)
所以h(x)在在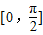 上为增函数,所以
上为增函数,所以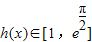 .
.
对k分类讨论:
①当k≤1时,g′(x)≥0恒成立,所以g(x)在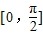 上为增函数,所以g(x)min=g(0)=0,
上为增函数,所以g(x)min=g(0)=0,
即g(x)≥0恒成立;
②当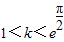 时,g′(x)=0在上有实根x,因为h(x)在
时,g′(x)=0在上有实根x,因为h(x)在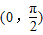 上为增函数,
上为增函数,
所以当x∈(0,x)时,g′(x)<0,所以g(x)<g(0)=0,不符合题意;
③当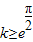 时,g′(x)≤0恒成立,所以g(x)在
时,g′(x)≤0恒成立,所以g(x)在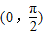 上为减函数,
上为减函数,
则g(x)<g(0)=0,不符合题意.
综合①②③可得,所求的实数k的取值范围是(-∞,1].
(3)因为F(x)=f(x)+excosx=ex(sinx+cosx),所以F′(x)=2excosx,
设切点坐标为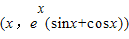 ,则斜率为
,则斜率为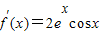 ,
,
切线方程为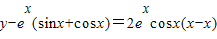 ,
,
将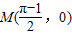 的坐标代入切线方程,得
的坐标代入切线方程,得
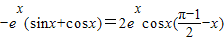
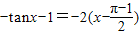 ,即
,即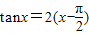 ,
,
令y1=tanx,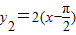 ,则这两个函数的图象均关于点
,则这两个函数的图象均关于点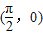 对称,
对称,
它们交点的横坐标也关于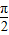 对称成对出现,
对称成对出现,
方程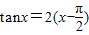 x∈
x∈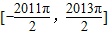 的根,
的根,
即所作的所有切线的切点横坐标构成的数列{xn}的项也关于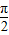 对称成对出现,
对称成对出现,
在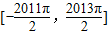 内共构成1006对,每对的和为π,
内共构成1006对,每对的和为π,
因此数列{xn}的所有项的和S=1006π.
点评:本题考查了利用导数研究函数的单调性,考查了利用导数求函数在闭区间上的最值,考查了数学转化思想方法和分类讨论的数学思想方法,训练了利用对称性求方程根的和的问题,综合考查了学生的计算能力,是具有较高难度的题目.
(2)构造辅助函数g(x)=f(x)-kx,把问题转化为求x∈
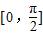 时g(x)min≥0,然后对k的值进行分类讨论,求k在不同取值范围内时的g(x)的最小值,由最小值大于等于0得到k的取值范围;
时g(x)min≥0,然后对k的值进行分类讨论,求k在不同取值范围内时的g(x)的最小值,由最小值大于等于0得到k的取值范围;(3)把f(x)的解析式代入F(x)=f(x)+excosx,求出函数F(x)的导函数,设出切点坐标,求出函数在切点处的导数,由点斜式写出切线方程,把M的坐标代入切线方程,得到关于切点横坐标的三角方程,利用函数图象交点分析得到切点的横坐标关于
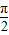 对称成对出现,最后由给出的自变量的范围得到数列{xn}的所有项之和S的值.
对称成对出现,最后由给出的自变量的范围得到数列{xn}的所有项之和S的值.解答:解:(1)由于f(x)=exsinx.所以
f′(x)=exsinx+excosx=
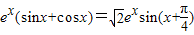 .
.当
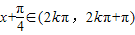 ,即
,即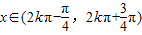 时,f′(x)>0;
时,f′(x)>0;当
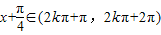 ,即
,即 时,f′(x)<0.
时,f′(x)<0.所以f(x)的单调递增区间为
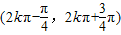 (k∈Z),
(k∈Z),单调递减区间为
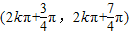 (k∈Z).
(k∈Z).(2)令g(x)=f(x)-kx=exsinx-kx,要使f(x)≥kx总成立,只需在x∈
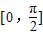 时g(x)min≥0.
时g(x)min≥0.对g(x)求导得g′(x)=ex(sinx+cosx)-k,
令h(x)=ex(sinx+cosx),则h′(x)=2excosx>0,(
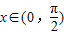 )
)所以h(x)在在
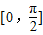 上为增函数,所以
上为增函数,所以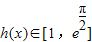 .
.对k分类讨论:
①当k≤1时,g′(x)≥0恒成立,所以g(x)在
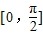 上为增函数,所以g(x)min=g(0)=0,
上为增函数,所以g(x)min=g(0)=0,即g(x)≥0恒成立;
②当
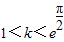 时,g′(x)=0在上有实根x,因为h(x)在
时,g′(x)=0在上有实根x,因为h(x)在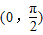 上为增函数,
上为增函数,所以当x∈(0,x)时,g′(x)<0,所以g(x)<g(0)=0,不符合题意;
③当
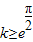 时,g′(x)≤0恒成立,所以g(x)在
时,g′(x)≤0恒成立,所以g(x)在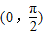 上为减函数,
上为减函数,则g(x)<g(0)=0,不符合题意.
综合①②③可得,所求的实数k的取值范围是(-∞,1].
(3)因为F(x)=f(x)+excosx=ex(sinx+cosx),所以F′(x)=2excosx,
设切点坐标为
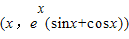 ,则斜率为
,则斜率为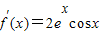 ,
,切线方程为
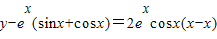 ,
,将
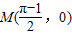 的坐标代入切线方程,得
的坐标代入切线方程,得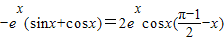
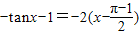 ,即
,即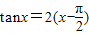 ,
,令y1=tanx,
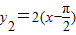 ,则这两个函数的图象均关于点
,则这两个函数的图象均关于点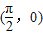 对称,
对称,它们交点的横坐标也关于
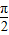 对称成对出现,
对称成对出现,方程
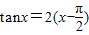 x∈
x∈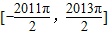 的根,
的根,即所作的所有切线的切点横坐标构成的数列{xn}的项也关于
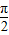 对称成对出现,
对称成对出现,在
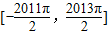 内共构成1006对,每对的和为π,
内共构成1006对,每对的和为π,因此数列{xn}的所有项的和S=1006π.
点评:本题考查了利用导数研究函数的单调性,考查了利用导数求函数在闭区间上的最值,考查了数学转化思想方法和分类讨论的数学思想方法,训练了利用对称性求方程根的和的问题,综合考查了学生的计算能力,是具有较高难度的题目.

练习册系列答案
相关题目