题目内容
(满分12分)已知函数
 的图象关于原点对称,
的图象关于原点对称, ,
,  为实数,
为实数,
(1)求 ,
, 的值;
的值;
(2)证明:函数 在
在 上是减函数;
上是减函数;
(3) 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
【答案】
(1)
(2)函数 在
在 上是减函数,证明略。
上是减函数,证明略。
(3)实数 的取值范围是
的取值范围是
【解析】
解:(1)∵ 的图象关于原点对称,∴
的图象关于原点对称,∴ 对一切实数均成立,即
对一切实数均成立,即

对 恒成立,比较系数,得
恒成立,比较系数,得
(2)由(1)知,
∴ ,由
,由 ,得
,得 ,
,
∴函数 在
在 上是减函数;
上是减函数;
(另证) (设 ,则
,则
 ∵
∵ www..com
www..com
∴ ,∴
,∴ ,
,
∴ ,即
,即 , ∴函数
, ∴函数 在
在 上是减函数;
上是减函数;
(3)由(2)知,函数 在
在 上是减函数,∴在区间
上是减函数,∴在区间 上,
上, ,
,
∴在区间 上,不等式
上,不等式 恒成立,就是
恒成立,就是
 成立,又由(1)知
成立,又由(1)知
∴ ,即
,即 或
或 ,
,
∴ ,即
,即 的取值范围是
的取值范围是 。
。

练习册系列答案
相关题目
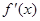 为f(x)的导函数,求证:
为f(x)的导函数,求证:

 的部分图象如图所示:
的部分图象如图所示: 的值;
的值; ,当
,当 时,求函数
时,求函数 的值域.
的值域.

